In this section, we will explore various solved problems related to proportionality. These problems are designed to illustrate how to identify and apply proportional relationships in different contexts. Through practical examples and detailed explanations, we will address how to solve proportionality problems using effective methods and techniques.
Calculate the unknown term in the following proportion

In a proportion, the product of the means equals the product of the extremes.


Calculate the unknown term in the following proportion

In a proportion, the product of the means equals the product of the extremes.

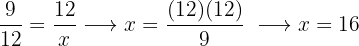
Calculate the unknown term in the following proportion
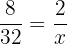
In a proportion, the product of the means equals the product of the extremes.
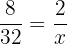
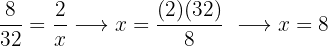
Calculate the unknown term in the following proportion
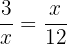
In a proportion, the product of the means equals the product of the extremes.
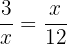
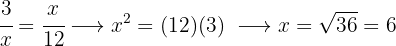
Calculate the unknown term in the following proportion

In a proportion, the product of the means equals the product of the extremes.

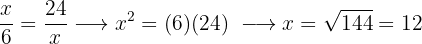
Two wheels are connected by a transmission belt. The first has a radius of 9.8 inches and the second of 29.5 inches. When the first has made 300 turns, how many turns will the second have made?
These are inversely proportional quantities, since a larger radius will make fewer turns

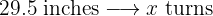
Then we have the following inverse proportion rule

Two gears are synchronized with each other. The first has 25 teeth and the second 10. When the second gear has made 50 turns, how many turns will the first have made?
These are inversely proportional quantities, since fewer teeth will make more turns
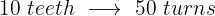

Then we have the following inverse proportion rule
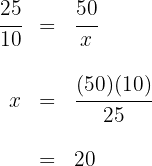
Four people cook 50 dishes in 3 hours. If one of the people gets sick, how long will it take the three people to prepare the 50 dishes?
Fewer people means more time, so this is an indirect proportion


Then we have the following indirect proportion rule
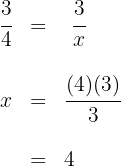
Six people can stay in a hotel for 12 days for $950. How much will the hotel cost for 15 people for eight days?
More people and more days means more money, so this is a direct proportion
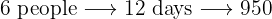
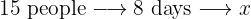
Then we have the following direct proportion rule
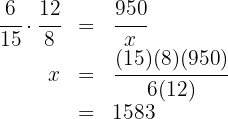
If with 12 cans of 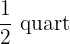 of paint each, 295 feet of fence 31.5 inches high have been painted. Calculate how many cans of
of paint each, 295 feet of fence 31.5 inches high have been painted. Calculate how many cans of 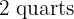 of paint will be needed to paint a similar fence
of paint will be needed to paint a similar fence 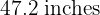 high and
high and 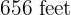 long.
long.
More quarts of paint means fewer cans, so this is an inverse proportion
More 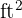 means more cans, so this is a direct proportion
means more cans, so this is a direct proportion
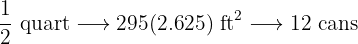
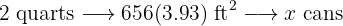
Then we have the following proportion rule
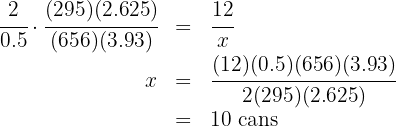
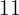 workers plow a rectangular field
workers plow a rectangular field 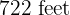 long and
long and 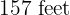 wide in
wide in  days. How many workers will be needed to plow another similar field
days. How many workers will be needed to plow another similar field 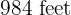 long by
long by 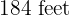 wide in five days?
wide in five days?
More surface area means more workers, so this is a direct proportion
More days means fewer workers, so this is an inverse proportion.
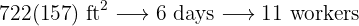
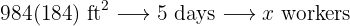
Then we have the following proportion rule
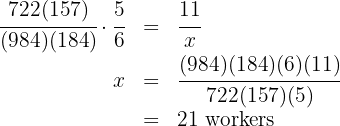
Six faucets take  hours to fill a tank with
hours to fill a tank with 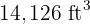 capacity. How many hours will four faucets take to fill
capacity. How many hours will four faucets take to fill 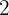 tanks of
tanks of 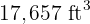 each?
each?
More faucets means fewer hours, so this is an inverse proportion.
More tanks means more hours, so this is a direct proportion.
More 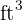 means more hours, so this is a direct proportion.
means more hours, so this is a direct proportion.

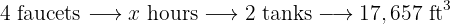
Then we have the following proportion rule

Of the  students in a school,
students in a school, 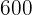 have gone on a trip. What percentage of students have gone on a trip?
have gone on a trip. What percentage of students have gone on a trip?
We will apply direct proportion
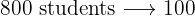
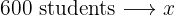
Then we have the following proportion rule
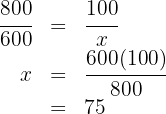
When purchasing a vehicle whose price is 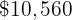 , we get a discount of
, we get a discount of 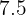 %. How much do we have to pay for the vehicle?
%. How much do we have to pay for the vehicle?
We start by doing the following proportion operation
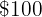
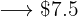
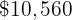
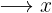
Then we have the following proportion rule
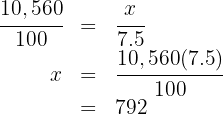
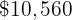 -
- 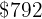
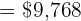
It can also be calculated directly as follows:
There is a discount of 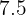 %, that is, for every
%, that is, for every 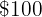 we pay
we pay 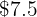 less, therefore instead of the
less, therefore instead of the 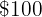 we pay
we pay 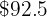 .
.
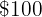
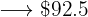
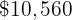
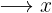
Then we have the following proportion rule
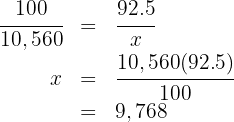
The price of a computer is 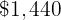 without tax. How much do we have to pay for it if the tax is
without tax. How much do we have to pay for it if the tax is  %?
%?
Due to tax there is a surcharge of  %, that is, for every
%, that is, for every 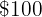 we pay
we pay 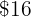 more, therefore instead of the
more, therefore instead of the 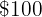 we pay
we pay 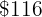
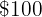
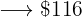
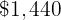
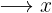
Then we have the following proportion rule
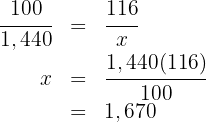
When buying a monitor that costs 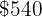 we get a discount of
we get a discount of 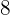 . How much do we have to pay?
. How much do we have to pay?
There is a discount of 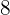 %, that is, for every
%, that is, for every 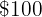 we pay
we pay 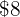 less, therefore instead of the
less, therefore instead of the 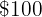 we pay
we pay 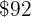 .
.
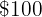
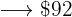
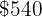
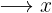
Then we have the following proportion rule
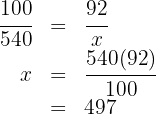
An item is sold with a profit of 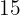 % over the cost price. If it was purchased for
% over the cost price. If it was purchased for 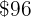 , find the selling price.
, find the selling price.
Due to profit there is a surcharge of 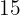 % over the cost price, that is, for every
% over the cost price, that is, for every 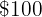 you pay
you pay 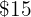 more, therefore instead of the
more, therefore instead of the 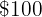 you pay
you pay 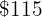
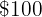
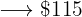
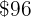
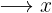
Then we have the following proportion rule
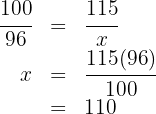
What price should we mark on an item whose purchase cost 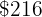 to gain
to gain 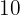 % when selling it?
% when selling it?
If the purchase price is 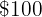 and you gain
and you gain 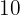 %, the selling price will be
%, the selling price will be 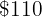 .
.
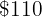
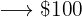
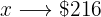
Then we have the following proportion rule
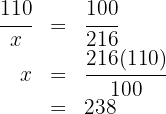
What selling price should we put on an item purchased for 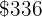 , to lose
, to lose 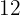 % on the selling price?
% on the selling price?
If the selling price is 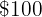 and you lose
and you lose 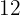 %, the purchase price will be
%, the purchase price will be 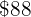 .
.
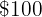
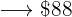
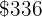
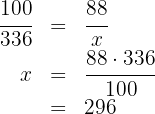
An object is sold losing 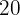 % on the purchase price. Find the selling price of said item whose purchase value was
% on the purchase price. Find the selling price of said item whose purchase value was 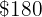 .
.
If the purchase price is 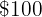 and you lose
and you lose 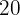 %, the selling price will be
%, the selling price will be 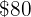 .
.
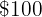
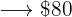
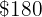
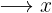
Then we have the following proportion rule
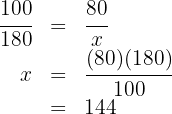
📌 Find the best math course on Superprof. Choose between an online math teacher or an in-person one for your classes.


