Welcome to our page dedicated to solved problems and exercises on quadratic equations! Here, we will explore the fascinating world of quadratic equations and provide you with the necessary tools to understand and solve these fundamental mathematical problems.
Quadratic equations are a fundamental part of mathematics and have wide application in various fields, such as physics, economics, and engineering. These equations are characterized by having an unknown raised to the second power and can have one or two real solutions.
Here, we will explore a wide variety of problems, from factorization problems to problems applying the quadratic formula, and we will provide you with clear and detailed explanations for each step of the solution process. Also, we will use these techniques to solve real-world situations.
Our goal is to help you develop your understanding of quadratic equations, strengthen your problem-solving skills, and foster your confidence in mathematics. So get ready to dive into the exciting world of quadratic equations and discover everything they have to offer!
Solve the following equations:
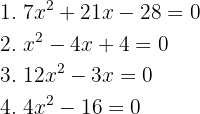
1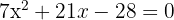 
It can be solved using the quadratic formula or the factorization method. Applying the factorization method:
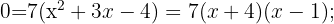
2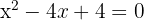 
Applying the factorization method:
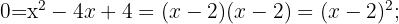
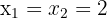
3 
Applying the factorization method:
4 
Applying the factorization method:
Solve the following equations:
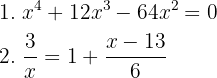
1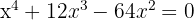 
Applying the factorization method:
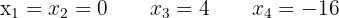
2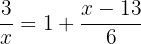 
We write the right-hand side with a common denominator and perform cross multiplication between each side by the denominators. Then, we apply the factorization method:
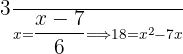
Solve the following equations:
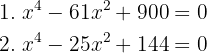
1 
Applying the factorization method, for example:
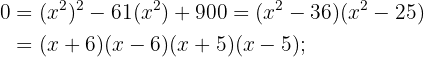
2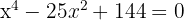 
Applying the factorization method:
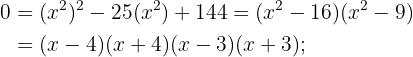
Solve the following equations:
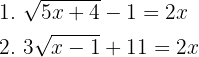
1 
First, we isolate the square root in the equation. Then, we square both sides of the equality, expand the powers, and solve.
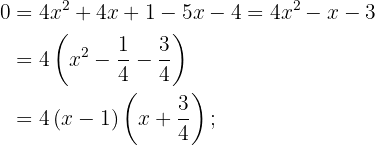
2 
We isolate the square root in the equation. Then, we square both sides of the equality, expand the powers, and solve using the quadratic formula.
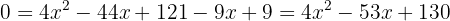
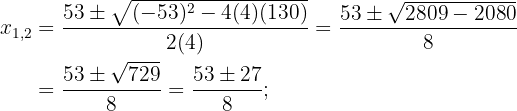
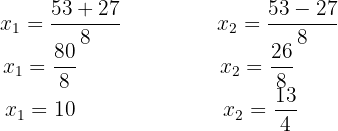
Find the roots of:
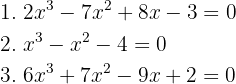
1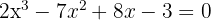 
We use synthetic division since the equation is of third degree. The divisors of 
are 
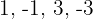. Thus:
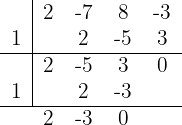
Therefore, the factorization is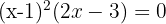 
. Hence:
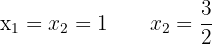
2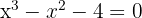 
We use synthetic division since the equation is of third degree. The divisors of 
are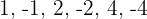 
. Thus:
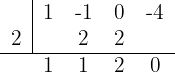
Therefore, the factorization is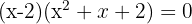 
. When calculating the discriminant of the trinomial, we conclude that it has no roots since the result is negative. Therefore, it has only one solution.
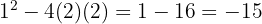
We use synthetic division since the equation is of third degree. The divisors of 
are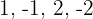 
. Thus:
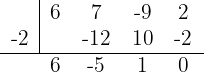
Therefore, the factorization is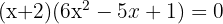 
. We solve the quadratic equation using the quadratic formula:
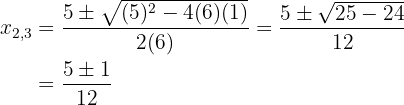
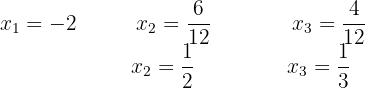
Solve the following systems of equations:
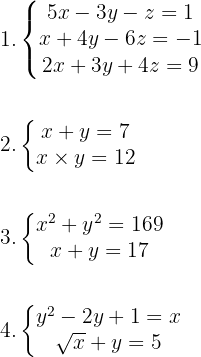
1
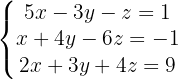
We construct the coefficient matrix associated with the system and reduce the columns and rows.
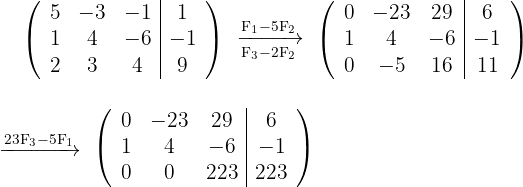
Therefore, 
. Translating the last matrix to the associated system of equations, we have that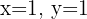 
, since:
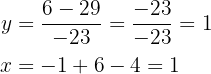
2
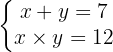
We solve for one unknown in the first equation and substitute the resulting expression into the second. Then, we solve the quadratic equation.
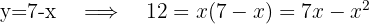
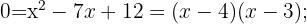
3
We solve for one unknown in the second equation and substitute the resulting expression into the first. Then, we solve the quadratic equation.
4
We substitute the expression that represents 
into the second equation. Then we square both sides of the equation and solve.
Determine the value of 
so that the solutions of the equation 
are the same value.
We calculate the discriminant and set it equal to zero. Thus, we obtain a double root.
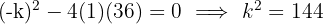
The possible values of the coefficient of the linear term are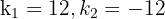 
.
Find the value of two numbers whose sum is five and their product is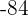 
.
The pairs of numbers are 
and 
.
Determine Pedro's age knowing that in 
years he will be half the square of the age he had 
years ago.
If we consider as his current age, years ago he was 
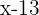and in years he will be 
:
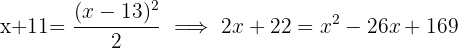
Therefore, Pedro is 
years old.
To fence a rectangular property of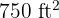 
, 
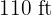of chain-link fencing was used. Calculate the dimensions of the property.
Dividing the amount of fencing used by two gives the semi-perimeter of the property,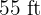 
. Therefore, the problem can be modeled with the expressions in the image:
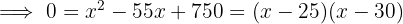
The property has dimensions of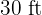 
y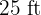 
.
The three sides of a right triangle are proportional to the numbers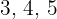 
. Calculate the length of each side of the triangle knowing that it has an area of 
.
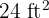The measures of the sides of the triangle are obtained by multiplying by a factor the sides of the right triangle in the image. From the formula to calculate the area, this factor can be determined.
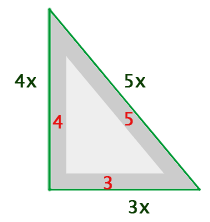
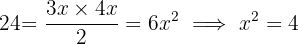
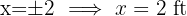
The sides of the triangle are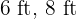 
and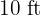 
.
A rectangular garden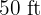 
long by 
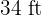wide is surrounded by a sand path of uniform width. Calculate the width of this path if it is known to have an area of 
.
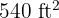When considering a width of the sand path, we have a larger rectangle with dimensions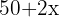 
by 
, as indicated by the figure. Now, we express the area of the sand path.
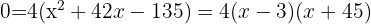
Therefore, the path is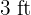 
wide.
Calculate the dimensions of a rectangle whose diagonal measures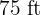 
knowing that it is similar to another rectangle of 
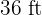by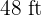 
.
Since the rectangle of 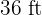by 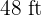is similar to the rectangle of 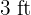by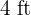 
, so will be the rectangle whose diagonal measures 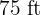. We assume, then, that its sides are proportional by a factor , as shown in the image. We apply the Pythagorean theorem and find the value of the unknown.
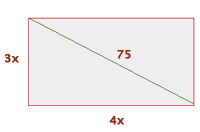
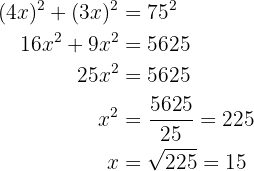
Therefore, the rectangle is approximately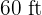 
long by 
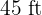wide.
Calculate two natural numbers whose difference is two and the sum of their squares is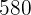 
.
Since the difference of these numbers is two, if denotes one number, the second will be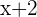 
.
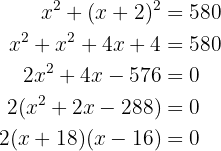
The numbers are 
and 
.
Two hoses A and B fill a pool together in two hours. A does it alone in three hours less than B. Calculate how many hours it takes each one to fill the pool.
If hose A takes hours to fill the pool, hose B will take 
hours to fill it. Then, each hour, A will have filled 
parts of the pool and B,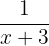 
parts. Since using both hoses fills the pool completely, we have:
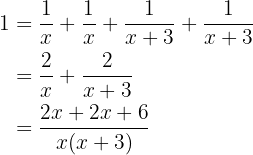
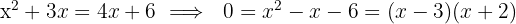
Hose A takes 
hours to fill the pool and hose B takes 
hours.
Find two numbers such that their product is four and the sum of their squares is seventeen.
We formulate the system of two equations with two unknowns and solve it.
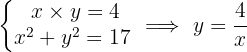
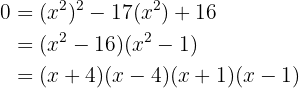
The possible pairs of numbers are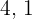 
and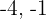 
.
Find a fraction equivalent to 
whose terms squared sum to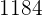 
.
We formulate the system of two equations with two unknowns and solve it.
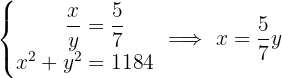
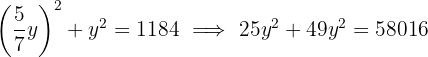
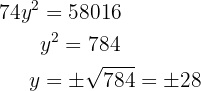
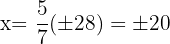
The fraction that satisfies the requirement is 
, since in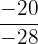 
the negative signs cancel and we obtain the first fraction.
A supermarket customer has paid a total of $171.60 for 24 gallons of milk, 6 lb of serrano ham, and 12 oz of olive oil. Calculate the price of each item, knowing that one ounce of oil costs triple what one gallon of milk costs and that one pound of ham costs the same as buying 4 oz of oil plus 4 gallons of milk.
We denote with 
the costs of milk, serrano ham, and olive oil, respectively. We form the related system of equations and solve it.
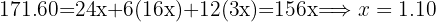
Milk costs $1.10 per gallon, serrano ham costs $17.60 per pound, and olive oil costs $3.30 per ounce.
A video store specializes in three types of movies: children's, westerns, and horror. It is known that:
60% of children's movies plus 50% of westerns represent 30% of the total movies. 20% of children's movies plus 60% of westerns plus 60% of horror movies represent half of the total movies.
Find the number of movies of each type knowing that there are 100 more westerns than children's movies.
We denote with the children's movies, westerns, and horror movies, respectively. We form the related system of equations and solve it.
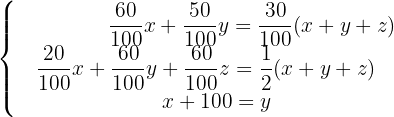
Simplifying the system of equations, we have:
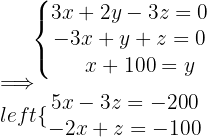
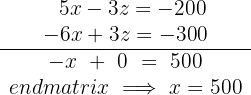
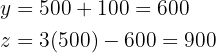
The video store has 500 children's movies, 600 westerns, and 900 horror movies.
Did you like this article? Rate it!
Loading...
