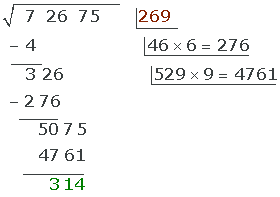Calculating square roots might seem intimidating at first, but with the right approach, it becomes much more manageable! There are several different methods you can use to find square roots, and this article will walk you through them step-by-step so you can choose the method that works best for you.

Steps to Find a Square Root
To solve a square root, we'll follow the steps using this example:
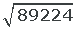
1 If the radicand has more than two digits, we separate the digits into groups of two, starting from the right.

2 We calculate the integer or exact square root of the first group of digits on the left, in this case the (8)

We ask ourselves: what number squared gives 8?
We see that 8 is not a perfect square, but it's between two perfect squares: 4 and 9
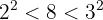
So we take the square root of the perfect square that's less than (8), which is the square root of 4, giving us 2, and we place it in the corresponding box.
3 The square of the obtained root 2 (that is 4) is subtracted from the first group of digits that appear in the radicand (8)
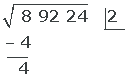
In other words, the square of 2 is 4, we subtract it from 8 and get 4.
4 We bring down the next group of digits from the radicand, separating the first digit on the right (2) from the formed number (492) and dividing what remains by double the root 2, that is 2(2)=4.
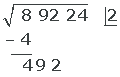
In other words:
- We bring down 92, making the operable quantity of the radicand: 492.
- We separate the 1st digit on the right (2) and we're left with 49.
- We divide 49 by double the previously obtained root 2 · 2 = 4
- Since the result of 49 ÷ 4 is greater than 9, we take 9 as the result
Note: We take 9 whenever the division result (49÷4) is greater than 9
5 In another row below the root we place double the same (4). Next, we place the obtained quotient (9). Then the obtained number (49) is multiplied by said quotient (9). After that, we subtract (441) from the operable quantity (492) of the radicand.
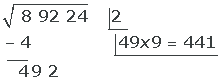
- We place double the root in another row, which in this case is 4.
- We place the obtained quotient (9) next to the 4, thus obtaining the number 49.
- We multiply 49 by 9 and get 441.
- We subtract 441 from 492 (which is the operable quantity of the result).
Note: If we had obtained a value greater than the operable quantity of the radicand, we would have tried 8, then 7… until finding a smaller value.
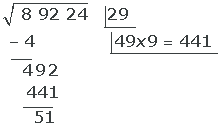
Note: If the result of doing 49 · 9 had been greater than 492, we would have tried doing 49 · 8, 49 · 7,…
6 The obtained quotient (9) is the second digit of the root, leaving (29).
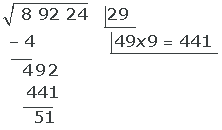
7 We bring down the next pair of digits and repeat the previous steps.
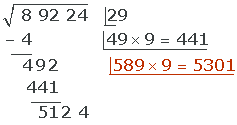
Since 5301 > 5124, we try 8.
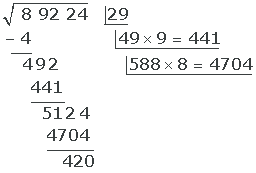
Finally, we bring up the 8 to the root.
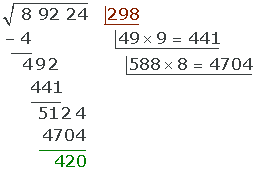
And with this we finish the process.
8 Square root verification. For the result to be correct, it must satisfy:

And indeed the obtained values satisfy it:
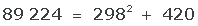
Square Root Examples
Solve the square roots of:
1 Calculate
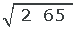
Applying the previous process, we obtain:
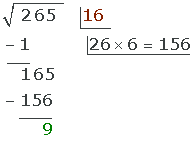
finishing the process
2 Calculate
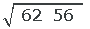
Let's see:
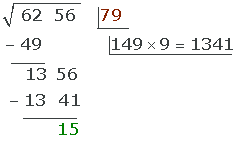
3 Calculate

Let's see: