Chapters

Explanation of The Substitution Method for Systems of Equations
The substitution method, as its name suggests, consists of substituting the value of a variable obtained from one of the equations and substituting it into the other equation. Systems of equations have a very important characteristic or rule: When a system of equations has more unknowns (variables) than the number of equations, then the system has infinite solutions, meaning each variable can take different values that always satisfy the equation, and the number of values each variable can take is infinite.
Given the equation
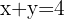
We observe that this is one equation with two variables. We can quickly realize some of the values that are solutions:
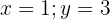
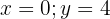
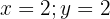
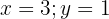

Note that there exists an infinite number of values we can assign to  and
and  for them to be solutions.
for them to be solutions.
On the other hand, when the system has more equations than unknowns, then the system has a unique solution.
Example of the Substitution Method
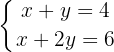
Equation I: 
Equation II: 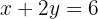
We solve for either of the 2 variables in one of the 2 equations (we should always look for the one that requires less algebraic work for our convenience). In this case, we will solve for  in Equation I.
in Equation I.
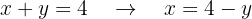
This is called "Value of  with respect to
with respect to  "
"
We substitute the solved value into the other equation. In this case, we substitute the value of  into Equation II
into Equation II

As we can notice, now the equation only contains the variable  . This equation can be simplified and solved to obtain the value of
. This equation can be simplified and solved to obtain the value of  .
.
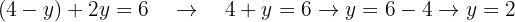
Once we have the value of one of the variables, in this case  , we can substitute it into either of the 2 equations to find the value of the other variable, in this case
, we can substitute it into either of the 2 equations to find the value of the other variable, in this case  .
.
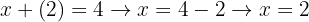
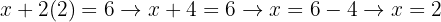
And thus we obtain the value of our variables in a system of equations and notice that the solution is UNIQUE.
Proposed Exercises for The Substitution Method
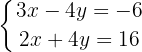
We solve for  in the second equation and simplify by dividing by 2
in the second equation and simplify by dividing by 2 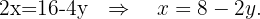
We substitute the value of variable  in the other equation and solve the equation
in the other equation and solve the equation 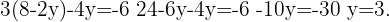
We substitute the value of  in the second equation
in the second equation 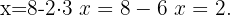
Therefore, the solution to the system of equations is 
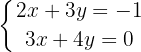
We solve for  from the second equation
from the second equation 
We substitute variable  in the other equation and solve the equation
in the other equation and solve the equation 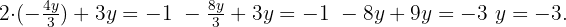
We substitute the value of  in the second equation
in the second equation 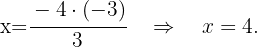
Therefore, the solution to the system of equations is 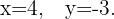
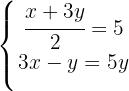
We eliminate denominators in the first equation by multiplying by 2 and rearrange the second 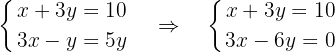
We solve for  in the second equation
in the second equation 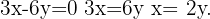
We substitute  in the other equation
in the other equation 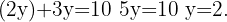
We substitute the value of  in the solved
in the solved 
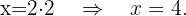
Therefore, the solution to the system of equations is 
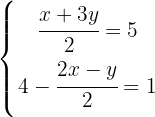
We eliminate denominators 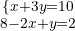
We operate in the second equation 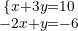
We solve for  in the first equation
in the first equation 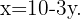
We substitute in the second equation and solve the equation 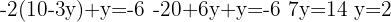
We substitute the value of  in the first equation
in the first equation 
Therefore, the solution to the system of equations is 
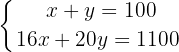
We solve for  in the first equation
in the first equation 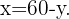
We substitute the value of  in the other equation and solve the equation
in the other equation and solve the equation 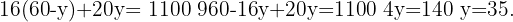
We substitute the value of  in the first equation
in the first equation 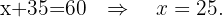
Therefore, the solution to the system of equations is 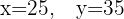
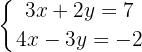
We solve for  in the first equation
in the first equation 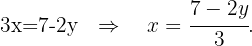
We substitute the value of  in the other equation and solve the equation
in the other equation and solve the equation 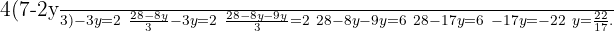
We substitute the value of  in the first equation
in the first equation 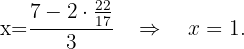
Therefore, the solution to the system of equations is 
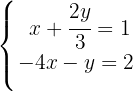
We solve for  in the first equation
in the first equation 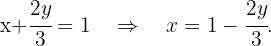
We substitute the value of  in the other equation and solve the equation
in the other equation and solve the equation 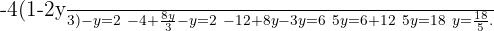
We substitute the value of  in the first equation
in the first equation 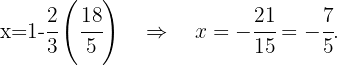
Therefore, the solution to the system of equations is 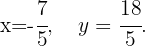
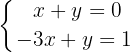
We solve for  in the first equation
in the first equation 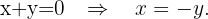
We substitute the value of  in the other equation and solve the equation
in the other equation and solve the equation 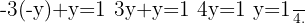
We substitute the value of  in the first equation
in the first equation 
Therefore, the solution to the system of equations is 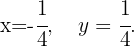
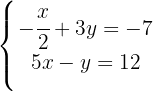
We solve for  in the first equation
in the first equation 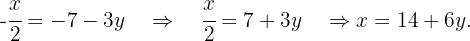
We substitute the value of  in the other equation and solve the equation
in the other equation and solve the equation 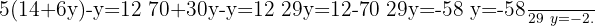
We substitute the value of  in the first equation
in the first equation 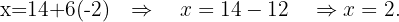
Therefore, the solution to the system of equations is 
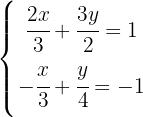
We solve for  in the first equation
in the first equation 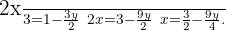
We substitute the value of  in the other equation and solve the equation
in the other equation and solve the equation 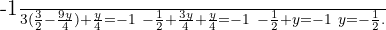
We substitute the value of  in the first equation
in the first equation 
Therefore, the solution to the system of equations is 












