The equalization method is an effective technique for solving systems of linear equations, especially those involving two variables. This method is based on isolating one of the variables in both equations and then equalizing the expressions obtained. This allows us to find a specific value for one of the variables, which can then be substituted to find the value of the other.

Equalization Method
The equalization method is based on the principle of transitivity.
If  and then
and then 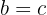 , then, by transitivity we know that
, then, by transitivity we know that  .
.
Example:
If 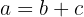 and we know that
and we know that  , then we can state that
, then we can state that 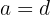 .
.
The same occurs in a system of equations using this method, as shown below.
Step 1: We select a variable that exists in each of the equations of the system.
Step 2: We isolate the variable in each of the equations.
Example:
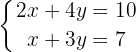
We can isolate either of the 2 variables, in this case we have chosen  . Remember to do it in each of the equations.
. Remember to do it in each of the equations.
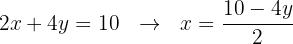

We can observe that both equations are equated with  , so by transitivity we say that:
, so by transitivity we say that:
If  and
and 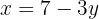 , then
, then 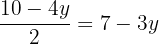 .
.
We can observe that now we only have one equation with one variable left, which we can simplify and isolate, obtaining:

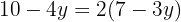
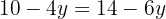

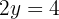

Now we substitute the value of y in either of the 2 equations to obtain the value of 
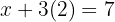
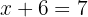


Proposed Exercises for the Equalization Method
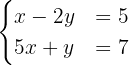
To solve by equalization we must isolate some variable from both equations. In this case we will isolate  . In the first equation we obtain:
. In the first equation we obtain:
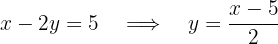
While for the second equation we obtain:
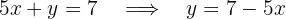
Equating the equations, we have

so that

so 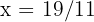 .
.
Then, substituting  in the second equation, we have
in the second equation, we have
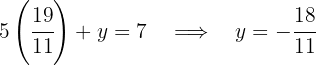
so 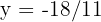 .
.
Thus, the solution is 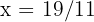 and
and 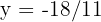 .
.
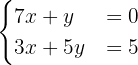
As in the previous case, to solve by equalization we must isolate some variable from both equations. In this case we will isolate  . In the first equation we obtain:
. In the first equation we obtain:
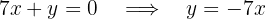
While for the second equation we obtain:
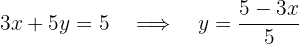
Equating the equations, we have
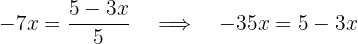
so 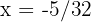 .
.
Then, substituting  in the first equation, we have
in the first equation, we have
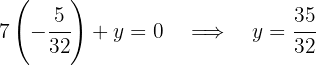
so 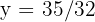 .
.
Thus, the solution is 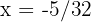 and
and 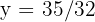 .
.
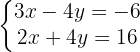
We isolate the unknown x from the first and second equation
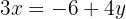

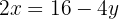
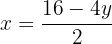
We equate both expressions
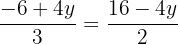
We solve the equation
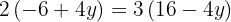
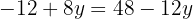
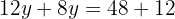


We substitute the value of  , in one of the two expressions in which we have isolated
, in one of the two expressions in which we have isolated  .
.
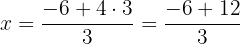
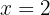
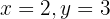

We isolate the unknown  from the first and second equation
from the first and second equation

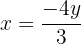
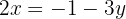
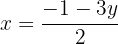
We equate both expressions

We solve the equation
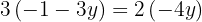
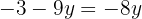

We substitute the value of y, in one of the two expressions in which we have isolated 

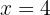
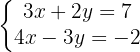
We isolate the unknown  from the first and second equation.
from the first and second equation.


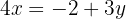

We equate both expressions and solve the equation
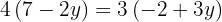
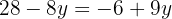

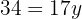

We substitute the value of y, in one of the two expressions in which we have isolated  .
.
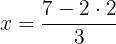

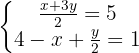
We multiply the second equation by 2, to simplify it:
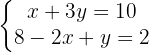
We arrange the terms
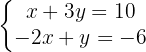
We isolate the unknown x from the first and second equation


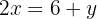
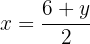
We equate both expressions and solve the equation
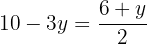

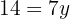

We substitute the value of  , in one of the two expressions in which we have isolated
, in one of the two expressions in which we have isolated  .
.
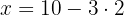
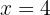
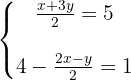
We clear denominators
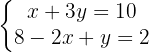
We arrange the second equation
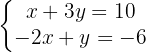
We isolate the unknown x from the first and second equation


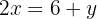
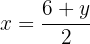
We equate both expressions
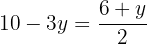
We solve the equation

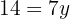

We substitute the value of  , in one of the two expressions in which
, in one of the two expressions in which  .
.
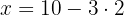
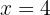
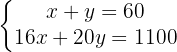
We isolate the unknown x from the first and second equation

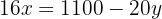
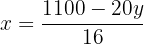
We equate both expressions
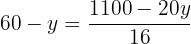
We solve the equation
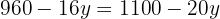
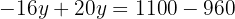

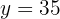
We substitute the value of  , in one of the two expressions in which we have isolated
, in one of the two expressions in which we have isolated  .
.


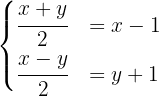
Before applying the equalization method, we must write the system in a way that allows us to isolate one of the variables. To do this, we multiply both equations by 2:

We isolate the variable y in both equations:

Equating the equations, we have

thus

so  . Then, substituting
. Then, substituting  in the first equation, we have
in the first equation, we have

so  . Thus, the solution is
. Thus, the solution is  and
and  .
.

First we isolate  from both equations
from both equations


Equating the equations, we have

so that

so  . Then, substituting
. Then, substituting  in the second equation, we have
in the second equation, we have

so  . Thus, the solution is
. Thus, the solution is  and
and  .
.












