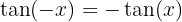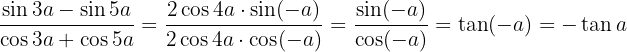Prove the Trigonometric Identities

We use the definition of tangent and cotangent to develop the left side of the equation

We use that  and the definitions of secant and cosecant to obtain
and the definitions of secant and cosecant to obtain

which is what we wanted to reach.

First we develop the square

We factor  from both addends, use the identity
from both addends, use the identity  and the definition of cosecant and cotangent
and the definition of cosecant and cotangent


We develop the right side, starting by factoring  from both addends
from both addends

We use the identity  and the definition of secant
and the definition of secant

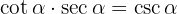
We use the definition of cotangent and secant
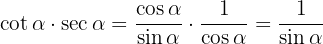
We cancel the factor 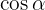 and use the definition of cosecant
and use the definition of cosecant
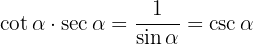
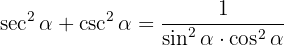
We develop with the definitions of secant and cosecant and operate the sum of fractions
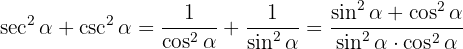
Finally we use the identity  and obtain the desired result
and obtain the desired result
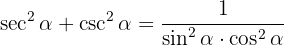
Prove Identities with Sum Formulas
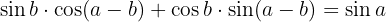
First we note that
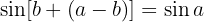
The sine sum formula is
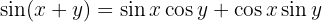
And using it we obtain the desired identity immediately
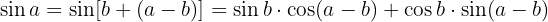
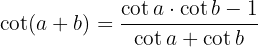
The definition of cotangent tells us that

We use the tangent sum formula and simplify

We divide the numerator and denominator by  , then use cotangent to reduce the expression
, then use cotangent to reduce the expression
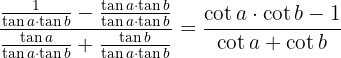
Simplify the Fractions
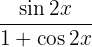
We use the double angle sine formula

We consider that since  then
then 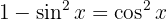
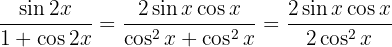
We simplify and apply the definition of tangent
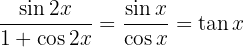
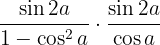
We substitute with  and the double angle sine formula and perform the fraction multiplication operation
and the double angle sine formula and perform the fraction multiplication operation
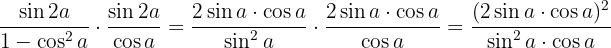
We develop and simplify
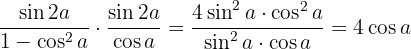
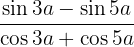
We use the formulas to convert from sums to products of trigonometric functions

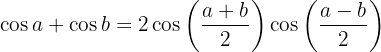
Then
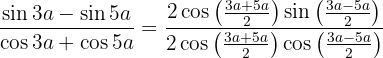
We simplify and use the definition of tangent. Also tangent is an odd function so