Below you will find a series of problems and exercises that are solved using trigonometry. In the solutions we describe in detail each of the steps performed.
Degree conversion.
Convert the following angles from radians to sexagesimal
a 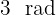
b 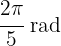
c 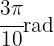
Let's remember that the formula to calculate an angle from radians to degrees is

where  is the angle in radians. Therefore, the angles in degrees are:
is the angle in radians. Therefore, the angles in degrees are:
a 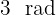
Here we have 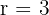 . Therefore, the degrees are
. Therefore, the degrees are
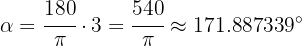
To obtain the minutes, we multiply the decimal part by 60:
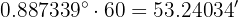
To obtain the seconds, we multiply the decimal part again by 60:
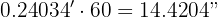
Therefore, the angle in sexagesimal form is 
b 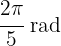
Just like in the previous exercise, we use the formula

c 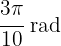
Here we also use the same formula:

Express the following angles in radians:
a 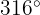
b 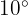
c 
The formula to convert from degrees to radians is very similar to the previous one
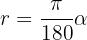
Thus, the angles are:
a 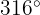
We use the formula
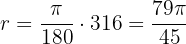
Therefore, the angle measures 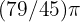 radians.
radians.
b 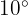
We use the formula
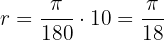
Therefore, the angle measures 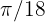 radians.
radians.
c 
We use the formula

This cannot be simplified since 127 is prime. Therefore, the angle measures 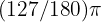 .
.
Convert the following angles from radians to sexagesimal
a 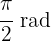
b 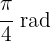
c 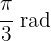
Let's remember that the formula to calculate an angle from radians to degrees is

where  is the angle in radians. Therefore, the angles in degrees are:
is the angle in radians. Therefore, the angles in degrees are:
a 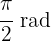
Here we have 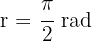 . Therefore, the degrees are
. Therefore, the degrees are
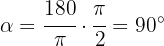
b 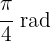
Just like in the previous exercise, we use the formula
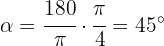
c 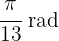
Here we also use the same formula:
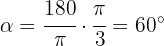
Express the following angles in radians:
a 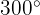
b 
c 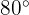
The formula to convert from degrees to radians is very similar to the previous one
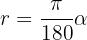
Thus, the angles are:
a 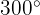
We use the formula
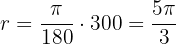
Therefore, the angle measures 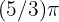 radians.
radians.
b 
We use the formula
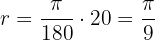
Therefore, the angle measures 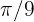 radians.
radians.
c 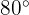
We use the formula
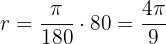
Therefore, the angle measures 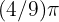 .
.
Convert the following angles from radians to sexagesimal
a 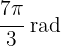
b 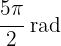
c 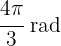
Let's remember that the formula to calculate an angle from radians to degrees is

where  is the angle in radians. Therefore, the angles in degrees are:
is the angle in radians. Therefore, the angles in degrees are:
a 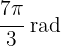
Here we have 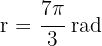 . Therefore, the degrees are
. Therefore, the degrees are
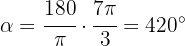
b 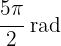
Just like in the previous exercise, we use the formula
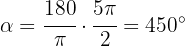
c 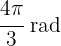
Here we also use the same formula:
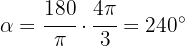
Express the following angles in radians:
a 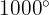
b 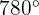
c 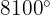
The formula to convert from degrees to radians is very similar to the previous one
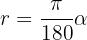
Thus, the angles are:
a 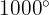
We use the formula
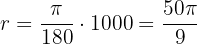
Thefore, the angle measures 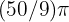 radians.
radians.
b 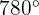
We use the formula
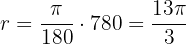
Therefore, the angle measures 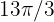 radians.
radians.
c 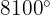
We use the formula
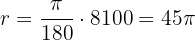
Therefore, the angle measures 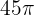 .
.
Calculating a trigonometric ratio from a given ratio.
Knowing that 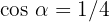 and that 0° <
and that 0° <  < 90^°, calculate
< 90^°, calculate 
We know that cosine is the ratio of the adjacent leg to the hypotenuse, so these are 1 and 4 respectively.
Applying the Pythagorean theorem we find the value of the leg opposite to 
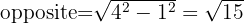
Thus, 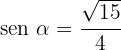
Knowing that 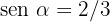 and that 0° <
and that 0° <  < 90°, calculate
< 90°, calculate 
We know that sine is the ratio of the opposite leg to the hypotenuse, so these are 2 and 3 respectively.
Applying the Pythagorean theorem we find the value of the leg adjacent to 
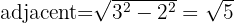
Thus, 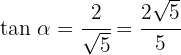
Knowing that 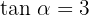 and that 0° <
and that 0° <  < 90°, calculate
< 90°, calculate 
We know that tangent is the ratio of the opposite leg to the adjacent leg, so these are 3 and 1 respectively.
Applying the Pythagorean theorem we find the value of the hypotenuse
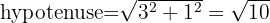
Thus, 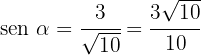
Knowing that 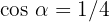 and that 270° <
and that 270° <  < 360°, calculate the remaining trigonometric ratios for angle
< 360°, calculate the remaining trigonometric ratios for angle 
First, we know that the angle is located in the fourth quadrant of the coordinate plane.
In this quadrant we have  but
but  . Therefore,
. Therefore,
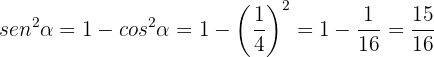
From this it follows that
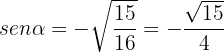
Since we now have  and
and  , the other identities are simpler.
, the other identities are simpler.

Note that both cotangent and cosecant can be rationalized. So it would also be correct if we had
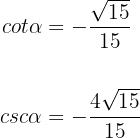
This is obtained by multiplying the previous results by  , thus avoiding radicals in the denominator.
, thus avoiding radicals in the denominator.
Knowing that 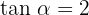 and that 180° <
and that 180° <  < 270°, calculate the remaining trigonometric ratios for angle
< 270°, calculate the remaining trigonometric ratios for angle 
The angle  is located in the 3rd quadrant of the coordinate plane. From this we know that
is located in the 3rd quadrant of the coordinate plane. From this we know that 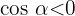 and
and 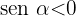 .
.
On the other hand, tangent is related to secant through its Pythagorean identity:
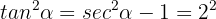
From which we have

Since 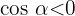 , thus
, thus 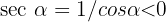 . Therefore,
. Therefore,
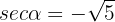
From this it follows that

Note that 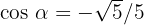 is also a correct answer (by rationalizing the previous result).
is also a correct answer (by rationalizing the previous result).
We also know that  . From this it follows that
. From this it follows that

The two remaining identities are calculated very simply:

and

Knowing that 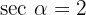 and that 0 <
and that 0 <  <
< 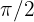 , calculate the remaining trigonometric ratios for angle
, calculate the remaining trigonometric ratios for angle 
Let's note, first, that the angle is in radians. Also, we are in the first quadrant of the coordinate plane, so 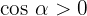 and
and  .
.
On the other hand, secant is related to  through its Pythagorean identity:
through its Pythagorean identity:
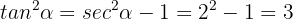
Furthermore, 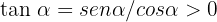 since
since  and
and  , thus
, thus
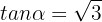
Similarly,
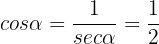
And since  , thus it follows that
, thus it follows that
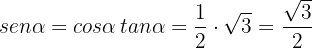
With this, the last two trigonometric identities are very simple to calculate:
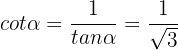
and

Calculating trigonometric ratios from angles.
Calculate the sine, cosine and tangent for the following angles:
a 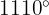
b 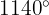
Here we will assume we have memorized the sine and cosine for some very common angles (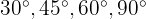 , etc.):
, etc.):
a 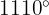
To calculate the sine of the angle, we will use some translation identities. Note that
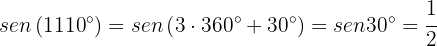
Similarly,
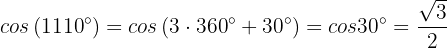
Finally
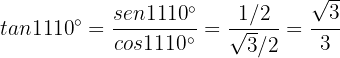
b 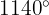
Just like in the previous case, we will use some translation identities. Note that
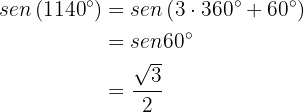
Similarly,
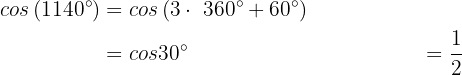
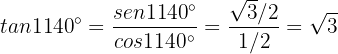
Calculate the sine, cosine and tangent for the following angles:
a 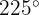
b 
Here we will assume we have memorized the sine and cosine for some very common angles (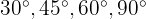 , etc.):
, etc.):
a 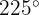
To calculate the sine of the angle, we will use some translation identities. Note that
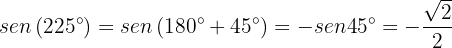
Similarly,

Finally

b 
Just like in the previous case, we will use some translation identities. Note that
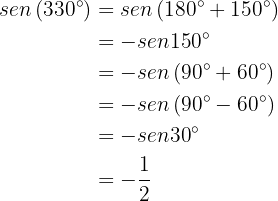
Similarly,
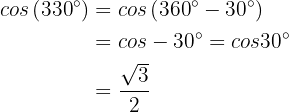

Calculate the trigonometric ratios for the following angles:
a 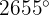
b 
a 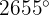
First we must find an angle that is between  and
and 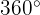 and that equals
and that equals 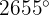 . To do this, we divide 2655 by 360 and the remainder will be the angle we're looking for:
. To do this, we divide 2655 by 360 and the remainder will be the angle we're looking for:

where the remainder is 135. Therefore
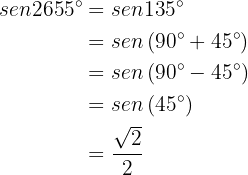
Similarly,
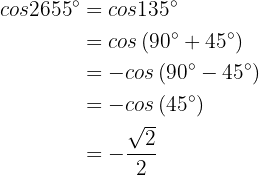
Finally,
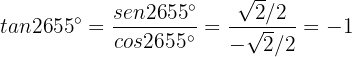
b
This is very similar to the previous case. We first divide 840 by 360 and keep the remainder:
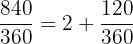
So 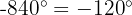 . Thus:
. Thus:
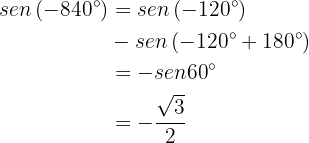
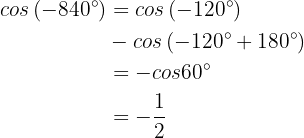
Finally,
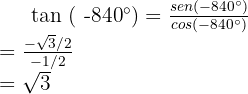
Triangle solving.
Given the right triangle ABC, right-angled at angle  , it is known that
, it is known that  (16.4 ft) and
(16.4 ft) and 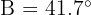 . Find the other angles and sides.
. Find the other angles and sides.
Let's observe the following triangle:
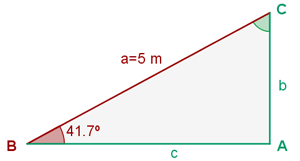
There we can see the data we're missing (sides  ,
,  and angle
and angle  ). The simplest is angle
). The simplest is angle  , since
, since  . Therefore
. Therefore
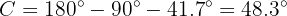
Since the triangle is right-angled, we can use trigonometric functions to calculate the length of the remaining sides. We know that

so
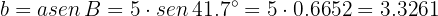
Similarly, since 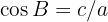 , then
, then

With this we have found all the missing data.
From triangle ABC, right-angled at angle  , we know that
, we know that 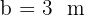 (9.8 ft) and
(9.8 ft) and 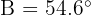 . Find the other angles and sides.
. Find the other angles and sides.
Let's observe the triangle from this exercise:
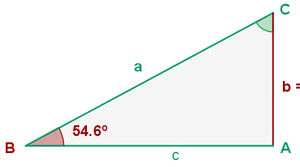
There we can see the data we're missing (sides  ,
,  and angle
and angle  ). Just like in the previous case, the simplest is angle
). Just like in the previous case, the simplest is angle  , since
, since  . Therefore
. Therefore
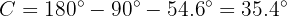
Now we don't have the hypotenuse. Therefore we must use tangent to start:
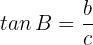
so
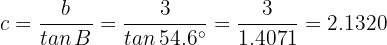
Similarly, since 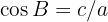 , then
, then
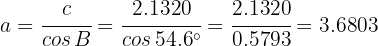
With this we have found all the missing data.
From triangle ABC, right-angled at angle  , we know that
, we know that  (19.7 ft) and
(19.7 ft) and 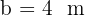 (13.1 ft). Find the acute angles and the remaining side.
(13.1 ft). Find the acute angles and the remaining side.
Let's observe the triangle:
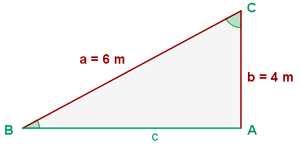
The data we're missing are leg  and angles
and angles  and
and  . By the Pythagorean theorem, we know that
. By the Pythagorean theorem, we know that  , so
, so
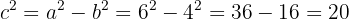
Thus, 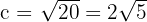 . Moreover,
. Moreover,
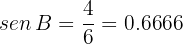
So 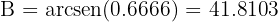 . Finally, since the angles sum to
. Finally, since the angles sum to 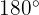 :
:
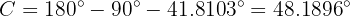
With this we finish solving the triangle.
Given triangle  , it is known that
, it is known that 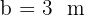 (9.8 ft),
(9.8 ft),  (16.4 ft) and
(16.4 ft) and 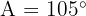 . Find the remaining angles and side.
. Find the remaining angles and side.
Note that this triangle is not right-angled. In fact, the triangle is shown in the following figure:
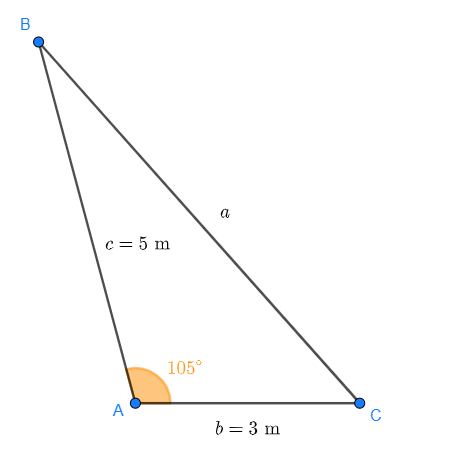
Where we see that we're missing angles  ,
,  and side
and side  . Since the triangle is not right-angled, we cannot use the Pythagorean theorem, but we can use the law of cosines:
. Since the triangle is not right-angled, we cannot use the Pythagorean theorem, but we can use the law of cosines:

where we already have all the data. We have
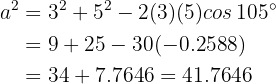
Therefore 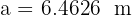 . With this, we can now calculate any of the remaining angles using the law of sines:
. With this, we can now calculate any of the remaining angles using the law of sines:

from which it follows that
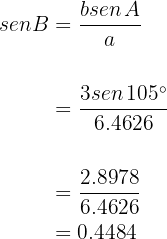
from which it follows that 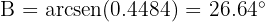 .
.
Finally,
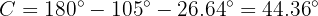
with which we solve the entire triangle completely.
Real-life problems.
A tree 50 meters (164 feet) tall casts a shadow 60 meters (197 feet) long. Find the angle of elevation of the Sun at that moment.
Note that the tree (side  ) and the shadow (side
) and the shadow (side  ) form the following triangle:
) form the following triangle:
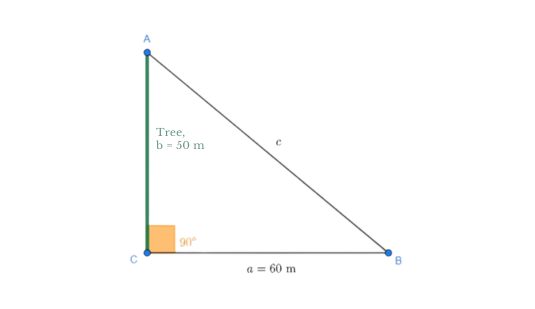
Notice that it's not necessary to calculate side  . We're looking for angle
. We're looking for angle  , whose tangent is given by
, whose tangent is given by

Using the arctangent, we obtain
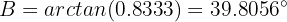
Which is the angle we were looking for.
An airship is flying at 800 meters (2,625 feet) altitude. It observes a town with a depression angle of 12°. What distance must the airship travel in a straight line, maintaining altitude, to be exactly over the town?
Note that between the town and the airship the following triangle is formed:
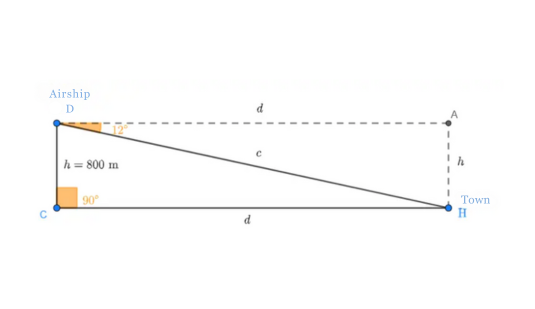
where we denote the unknown distance by  . We denote the airship's altitude by
. We denote the airship's altitude by  and the depression angle coincides with angle
and the depression angle coincides with angle  .
.
We know that the tangent of 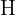 is calculated using
is calculated using

so
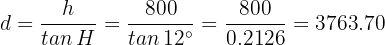
Therefore, the airship must travel 3,763.70 meters, or 2.34 miles.
Find the radius of a circle where a chord of 24.6 meters (80.7 feet) has a corresponding arc of 70°.
Let's observe the following figure:
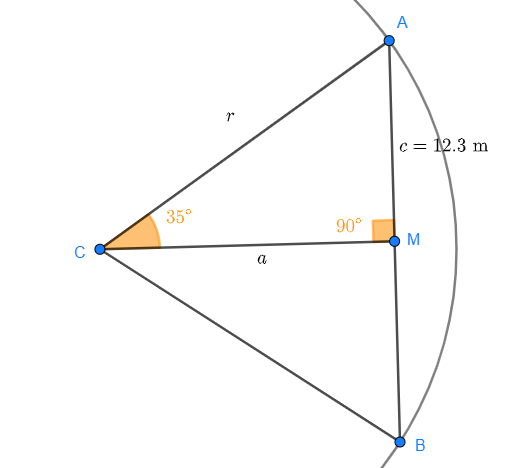
Notice that a right triangle is formed with points 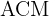 where
where  is the midpoint of the arc.
is the midpoint of the arc.
The radius  is the hypotenuse of this triangle, the length of
is the hypotenuse of this triangle, the length of  is half the chord, that is,
is half the chord, that is,
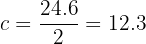
and angle  measures
measures  (half the arc). We know that
(half the arc). We know that

since  is the hypotenuse. Therefore,
is the hypotenuse. Therefore,

Therefore, the radius measures 21.44 meters (70.3 feet).
Calculate the area of a triangular plot, knowing that two of its sides measure 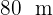 (262 ft) and
(262 ft) and 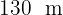 (427 ft), and the angle between them is 70°.
(427 ft), and the angle between them is 70°.
There are several ways to solve this problem. We can use Heron's formula or we can try to calculate one of its heights. First let's observe the triangle:
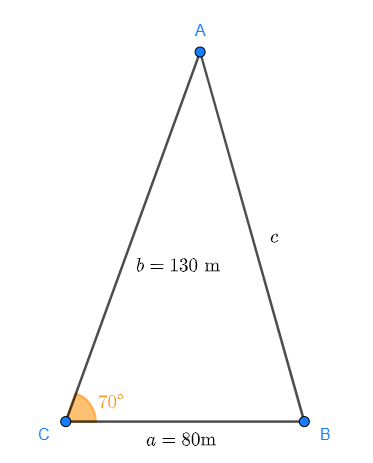
Where 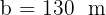 ,
, 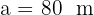 and
and 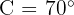 .
.
If we draw the height that is perpendicular to  , notice that a right triangle is formed where
, notice that a right triangle is formed where  is a leg and
is a leg and  is the hypotenuse. Also, notice that the sine of
is the hypotenuse. Also, notice that the sine of  is
is
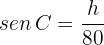
so
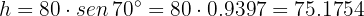
Therefore, the area is
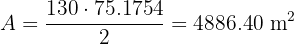
Calculate the height of a tree, knowing that from a point on the ground its top is observed at an angle of 30° above ground level, and if we move 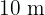 (32.8 ft) closer then the top is observed at an angle of 60° above the ground.
(32.8 ft) closer then the top is observed at an angle of 60° above the ground.
Let's observe the following figure, which is a representation of the problem:
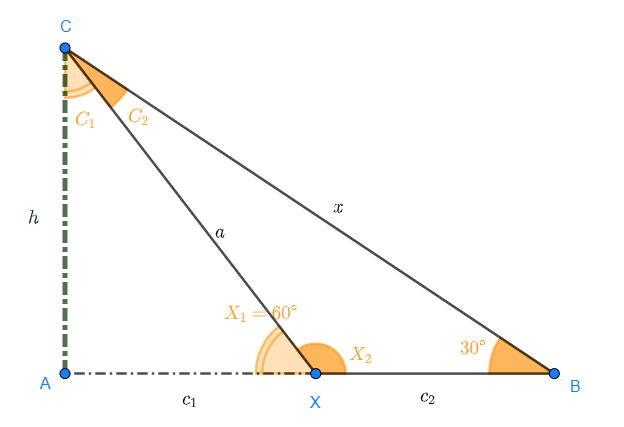
Notice that there are several ways to solve this problem. One is to find the distance 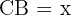 by solving triangle
by solving triangle  ; then we use that distance to find the height.
; then we use that distance to find the height.
To solve the triangle, notice that angle 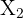 of triangle
of triangle  is
is
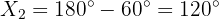
therefore, we can now use the law of sines to solve the triangle. However, we first need angle 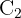 , which is,
, which is,

By the law of sines we have
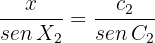
where
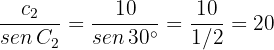
Therefore,
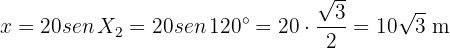
With this we can now calculate the height of the tree. Notice that triangle  is right-angled. Therefore,
is right-angled. Therefore,
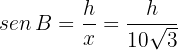
Thus,

Therefore, the tree is 8.66 meters (28.4 feet) tall.
A regular octagon has sides that measure 12 meters (39.4 feet). Find the radii of the inscribed and circumscribed circles.
Look at the following figure of an octagon with its inscribed and circumscribed circles:
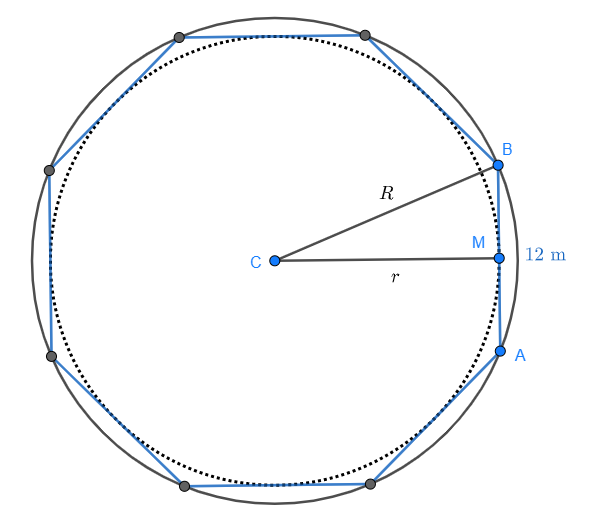
Notice that a right triangle is formed between points  where
where  is the midpoint of any side of the octagon. Let's observe this right triangle in more detail:
is the midpoint of any side of the octagon. Let's observe this right triangle in more detail:
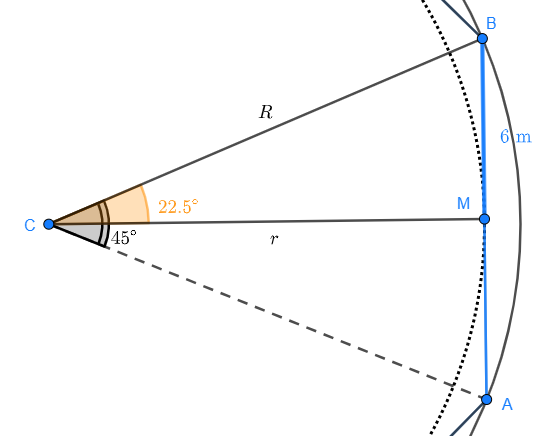
We know that angle 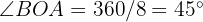 . So angle
. So angle  of the right triangle will be
of the right triangle will be 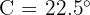 . Also, side
. Also, side 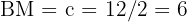 .
.
The two sides of the triangle we're missing are, in fact, the radii of the circles. Starting with side  , we have
, we have

So
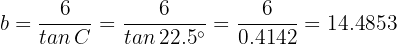
Therefore, the radius  of the inscribed circle is 14.49 meters (47.5 feet).
of the inscribed circle is 14.49 meters (47.5 feet).
Then, side  satisfies
satisfies

so 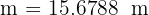 . That is, the radius
. That is, the radius  of the circumscribed circle is 15.68 meters (51.4 feet).
of the circumscribed circle is 15.68 meters (51.4 feet).
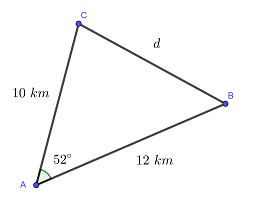
Three cities  and
and  are distributed in a triangular formation and their roads are straight lines. If the distance from
are distributed in a triangular formation and their roads are straight lines. If the distance from  to
to  is 12 km (7.5 miles), the distance from
is 12 km (7.5 miles), the distance from  to
to  is 10 km (6.2 miles) and angle
is 10 km (6.2 miles) and angle 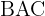 is
is 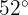 . Find the distance between cities
. Find the distance between cities  and
and  .
.
The figure representing the problem forms a triangle
Notice that to calculate side 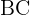 we just need to apply the law of cosines
we just need to apply the law of cosines

Performing the operations, we obtain
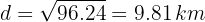
Which is the distance between cities  and
and  that we were looking for.
that we were looking for.
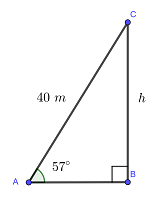
Peter flies a kite for which he uses 40 m (131 ft) of string. If the elevation angle is 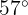 , what is the height of the kite above the ground?
, what is the height of the kite above the ground?
Notice that the kite string (side  ) and the projection of the kite to the ground (side
) and the projection of the kite to the ground (side  ) form the following right triangle:
) form the following right triangle:
Notice that the expression for the sine of angle  is:
is:
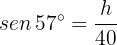
Solving for height  , we obtain
, we obtain
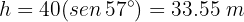
Which is the height we were looking for.
A building casts a shadow 60 meters (197 ft) long, with 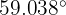 being the sun's elevation angle at that moment. Find the height of the building.
being the sun's elevation angle at that moment. Find the height of the building.
Notice that the building (side 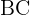 ) and the shadow (side
) and the shadow (side 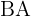 ) form the following right triangle:
) form the following right triangle:
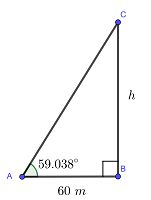
Notice that the expression for the tangent of the 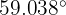 angle is given by
angle is given by
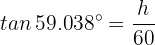
Solving for height  , we obtain
, we obtain

Which is the height we were looking for.
Proof of trigonometric identities.
Prove the following trigonometric identities:
a 
b 
c 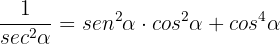
a 
We start by writing 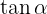 and
and 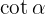 with their definition in sines and cosines:
with their definition in sines and cosines:

Then we perform the addition of fractions (with the common denominator):

We notice that 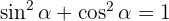 , so
, so

which are the definitions of 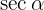 and
and  . Therefore,
. Therefore,
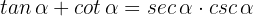
b 
Here it's convenient to start from the right side of the equation:

We factor out 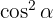
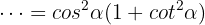
Let's remember that the Pythagorean identity for 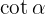 is
is 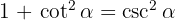 , so we have
, so we have
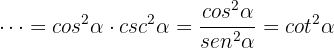
which was exactly what we wanted to prove.
c 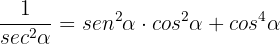
Here it's also convenient to start from the right side of the identity, factoring 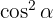 :
:
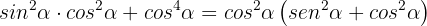
We notice that 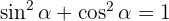 , so
, so
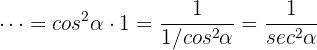
which was what we were looking to prove.
Prove the following trigonometric identities:
a 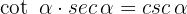
b 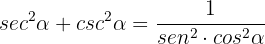
a 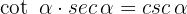
The simplest way to prove this identity is to start from the left side and write the relationships in terms of sines and cosines:

since  cancels out. This identity could be proven in a single line.
cancels out. This identity could be proven in a single line.
b 
We start from the left side and write the relationships in terms of sines and cosines:
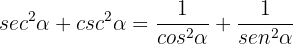
Then we add the fractions using the common denominator:
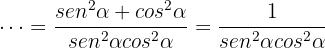
since 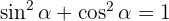 . Therefore, we arrive at what we wanted to prove.
. Therefore, we arrive at what we wanted to prove.


