Uniform circular motion (UCM) is a special type of motion in which an object moves around a fixed point with constant speed and a circular path. In this type of motion, the magnitude of the velocity does not change, but the direction of the velocity is constantly changing, which results in continuous motion around a circle.
To better understand the concepts associated with UCM, it is essential to work through a series of exercises that address key aspects such as angular velocity, centripetal acceleration, period, and frequency. Through solving these exercises, you will be able to deepen your theoretical understanding and develop practical skills related to uniform circular motion.
A particle rotates in a horizontal circle, completing two full revolutions per second. Determine the period of the particle.
The period  is the time to complete one revolution (turn) of the particle in the circle.
is the time to complete one revolution (turn) of the particle in the circle.
Since the particle completes two revolutions per second, then one revolution is completed in 0.5 seconds.
Thus, the period is 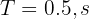
A particle rotating in a horizontal circle has a period of 0.25 seconds. Calculate its frequency of rotation.
The frequency of rotation 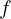 is the reciprocal of the period
is the reciprocal of the period
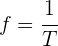
Thus, the frequency of rotation is
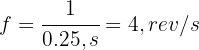
An object is made to rotate in a horizontal circle by means of a string 4 feet long. If the object has a period of 1/3 of a second, what is its linear speed?
1. The known data are:
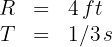
2. To calculate the linear velocity, we use the formula

3. We substitute the known data into the formula and obtain
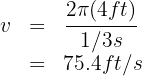
An object moves on a circular track with a radius of 15 feet and frequency of 2 revolutions per second. Find the linear velocity.
1. The known data are:
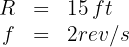
2. To calculate the linear velocity, we use the formula
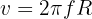
3. We substitute the known data into the formula and obtain
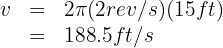
A particle moves on a circle with a radius of 12 inches and completes 5 revolutions per second. Determine its linear velocity and centripetal acceleration.
1. The known data are:
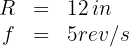
We convert the radius to feet
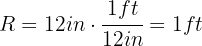
2. To calculate the linear velocity, we use the formula
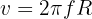
3. We substitute the known data into the formula and obtain
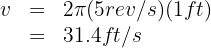
4. To calculate the centripetal acceleration, that is, the acceleration that always points toward the center, we use the formula
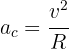
5. We substitute the known data into the formula and obtain
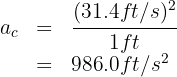
A 1,800-pound car moves on a circular track with a diameter of 160 feet, completing 3 laps every 2 minutes. What is its centripetal force?
1. The known data are:
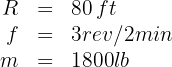
We write the revolutions in seconds
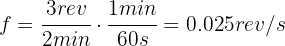
2. To calculate the linear velocity, we use the formula
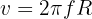
3. We substitute the known data into the formula and obtain
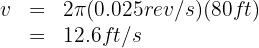
4. To calculate the centripetal acceleration, that is, the acceleration that always points toward the center, we use the formula
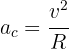
5. We substitute the known data into the formula and obtain
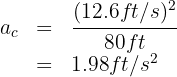
6. We substitute the known data into the centripetal force formula and obtain (converting mass to slugs: 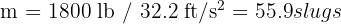 )
)
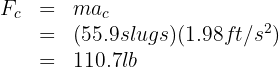
The wheel of a car has an 8-inch radius and rotates 4 revolutions in 1 second. What is its angular velocity? What linear distance does the car travel in 1 minute?
1. The known data are:
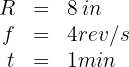
We write the radius in feet and the time in seconds
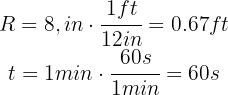
2. To calculate the angular velocity, we use the formula
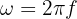
3. We substitute the known data into the formula and obtain
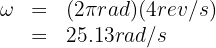
4. To calculate the linear distance, we use the formula
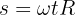
5. We substitute the known data into the formula and obtain
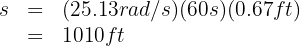
A particle performs circular motion with an angular velocity of 18.85 rad/s. What is the number of revolutions in 1 minute?
1. The known data are:
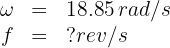
2. To calculate the frequency, we use the formula
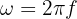
3. We substitute the known data into the formula and obtain
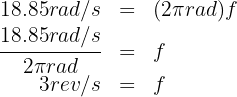
4. The number of revolutions in one minute is
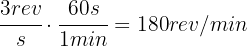
The wheel of a bicycle has a 10-inch radius with an angular velocity of 5 rad/s. How long does it take to complete one full revolution?
1. The known data are:
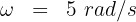
2. Calculate the frequency, using the formula
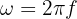
3. We substitute the known data into the formula and obtain
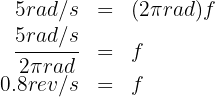
4. The time it takes the wheel to complete one revolution equals the period

A bicycle rotates on a circular track with a radius of 50 feet, with an angular velocity of 5.24 rad/s. What is its centripetal acceleration?
1. The known data are:
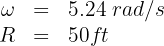
2. To calculate the centripetal acceleration, we use the formula
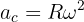
3. We substitute the known data into the formula and obtain
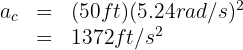
Summarize with AI:


