A vector has initial and final endpoints 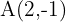 and
and 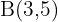 respectively. Find the coordinates of
respectively. Find the coordinates of 
We know that the coordinates of a vector are obtained by subtracting the initial point from the final point
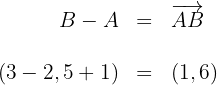
A vector has final and initial endpoints 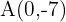 and
and 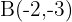 respectively. Find the coordinates of
respectively. Find the coordinates of 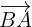
We know that the coordinates of a vector are obtained by subtracting the initial point from the final point
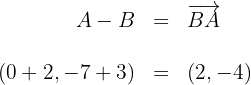
A vector  has components
has components 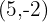 . Find the coordinates of
. Find the coordinates of  if endpoint
if endpoint 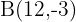 is known
is known
1 Since we don't know the coordinates of  , we denote them by
, we denote them by
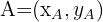 .
.
2 We know that the coordinates of a vector are obtained by subtracting the initial point from the final point
3 We obtain two equations
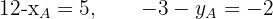
4 We solve both equations and obtain that the coordinates of  are
are
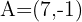
A vector  has components
has components 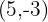 . Find the coordinates of
. Find the coordinates of 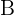 if endpoint
if endpoint 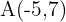 is known
is known
1 Since we don't know the coordinates of 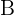 , we denote them by
, we denote them by 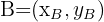 .
.
2 We know that the coordinates of a vector are obtained by subtracting the initial point from the final point
3 We obtain two equations 
4 We solve both equations and obtain that the coordinates of 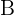 are
are
Given the vector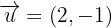 and two vectors equivalent to
and two vectors equivalent to  and
and 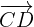 , determine
, determine 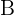 and
and 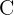 knowing that
knowing that 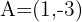 and
and 
1 Since  are equivalent, then
are equivalent, then 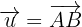 .
.
2 Since we don't know the coordinates of 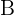 , we denote them by
, we denote them by
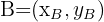 .
.
3 We know that the coordinates of a vector are obtained by subtracting the initial point from the final point
4 We obtain two equations

5 We solve both equations and obtain that the coordinates of 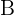 are
are

6 Solving in the same way as for 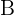 , we have that
, we have that  .
.
Calculate the distance between points 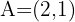 and
and 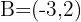
1 The formula for the distance between two points is

2 We substitute the values of  and
and 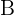 in the distance formula between two points and obtain
in the distance formula between two points and obtain
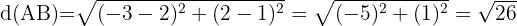
Calculate the distance between points 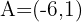 and
and 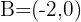
1 The formula for the distance between two points is 
2 We substitute the values of  and
and 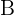 in the distance formula between two points and obtain
in the distance formula between two points and obtain 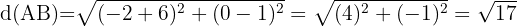
Find the value of  so that the distance between points
so that the distance between points 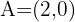 and
and 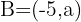 is 7
is 7
1 The formula for the distance between two points is 
2 We substitute the values of  and
and 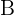 in the distance formula between two points and obtain
in the distance formula between two points and obtain 
3 Squaring both sides and solving, we obtain 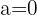
Find the value of  so that the distance between points
so that the distance between points 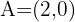 and
and 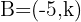 is 8
is 8
1 The formula for the distance between two points is 
2 We substitute the values of  and
and 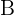 in the distance formula between two points and obtain
in the distance formula between two points and obtain 
3 Squaring both sides and solving, we obtain 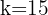
If  is a vector with components
is a vector with components 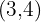 , find a unit vector with the same direction and sense
, find a unit vector with the same direction and sense
1 The formula for a unit vector is
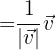
2 We calculate the magnitude of 
3 We substitute into the formula to obtain a unit vector

If  is a vector with components
is a vector with components 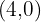 , find a unit vector with the same direction and opposite sense
, find a unit vector with the same direction and opposite sense
1 The formula for a unit vector is 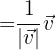
2 We calculate the magnitude of 
3 We substitute into the formula to obtain a unit vector 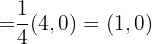
4 We are asked for the unit vector to have opposite sense, that is 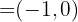
Find a unit vector with the same direction as the vector 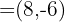
1 The formula for a unit vector is
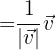
2 We calculate the magnitude of 
3We substitute into the formula to obtain a unit vector
Calculate the coordinates of  so that the quadrilateral with vertices
so that the quadrilateral with vertices  and
and  is a parallelogram.
is a parallelogram.
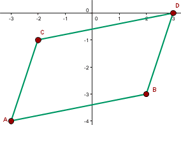
1 The opposite sides of a parallelogram are equal in magnitude and direction, so we have
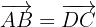
2 Since we don't know the coordinates of 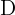 , we denote them by
, we denote them by
 .
.
3 We substitute the values of the vertices of the parallelogram into the vector equality
4 We obtain two equations

5 Solving the equations we obtain the sought coordinates

Find the coordinates of the midpoint of segment 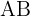 , with endpoints
, with endpoints  and
and  .
.
1 The formulas for the coordinates of the midpoint are

2 We substitute the values of  and
and 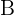 into the two previous formulas
into the two previous formulas
3 The midpoint is 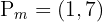 .
.
Find the coordinates of point 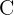 , knowing that
, knowing that 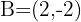 is the midpoint of
is the midpoint of  , where
, where 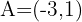 .
.
1 The formulas for the coordinates of the midpoint are

2 We substitute the values of  and
and 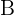 into the two previous formulas and calculate the first coordinate of
into the two previous formulas and calculate the first coordinate of 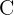
3 The second coordinate of 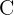 is
is
4 Finally 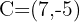
Determine whether points  and
and  are collinear.
are collinear.
1 Points 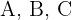 are collinear if the slopes of segments
are collinear if the slopes of segments 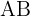 and
and  are equal.
are equal.

2 Since both slopes are equal, then the three points are collinear.
Determine whether points 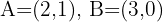 and
and 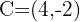 are collinear.
are collinear.
1 Points 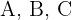 are collinear if the slopes of segments
are collinear if the slopes of segments 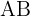 and
and  are equal.
are equal.
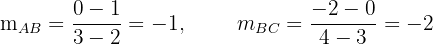
2 Since both slopes are not equal, then the three points are not collinear.
Calculate the value of  so that points
so that points 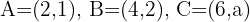 are collinear.
are collinear.
1 Points 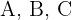 are collinear if the slopes of segments
are collinear if the slopes of segments 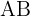 and
and  are equal.
are equal.
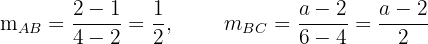
2 Since both slopes are equal, we equate both expressions and solve for 
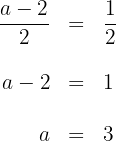
Given points 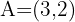 and
and 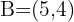 , find a point
, find a point 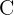 collinear with
collinear with  and
and 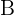 , such that
, such that 
1 We start from the given condition and obtain an equality
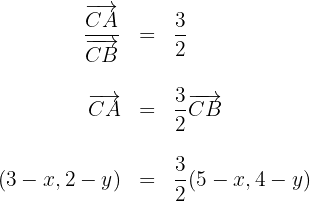
2 We equate both expressions coordinate by coordinate and obtain
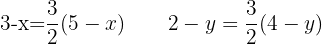
3 We solve both equations to obtain the coordinates of 
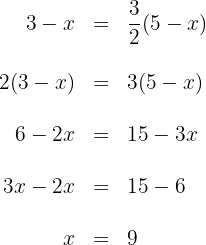
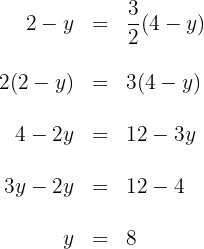
Given a triangle with vertices 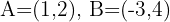 and
and  , find the coordinates of the centroid
, find the coordinates of the centroid
1 The formula to find the centroid is

2 Substituting the values of the vertices of the triangle we obtain

Given a triangle with two of its vertices 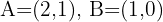 and the centroid
and the centroid 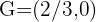 , calculate the third vertex
, calculate the third vertex
1 The formula to find the centroid is

2 Substituting the values of the centroid and the vertices of the triangle we obtain two equations

3 We solve both equations and obtain the third vertex 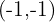 .
.
Find the symmetric point of 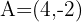 with respect to
with respect to 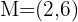
1 We denote by 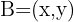 the symmetric point of
the symmetric point of  , then it holds that
, then it holds that 
2 Substituting the values of the points, we obtain two equations corresponding to the coordinates of the vectors

3 We solve both equations and obtain  .
.
Find the symmetric point of  with respect to
with respect to 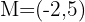
1 We denote by 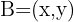 the symmetric point of
the symmetric point of  , then it holds that
, then it holds that 
2 Substituting the values of the points, we obtain two equations corresponding to the coordinates of the vectors

3 We solve both equations and obtain 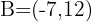 .
.
What points  and
and  divide the segment with endpoints
divide the segment with endpoints 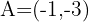 and
and 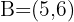 into three equal parts?
into three equal parts?
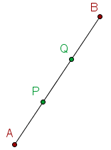
1 In vector notation we have

2 Substituting the values of the points, we obtain two equations corresponding to the coordinates of the vectors

3 We solve both equations and obtain 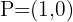 .
.
4 To find the coordinates of  we use the condition
we use the condition
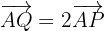
5 Substituting the values of the points, we obtain two equations corresponding to the coordinates of the vectors
6 We solve both equations and obtain 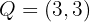 .
.
If segment 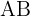 with endpoints
with endpoints 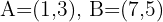 is divided into four equal parts, what are the coordinates of the division points?
is divided into four equal parts, what are the coordinates of the division points?
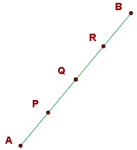
1 We note that  is the midpoint of segment
is the midpoint of segment 
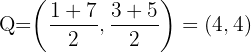
2  is the midpoint of segment
is the midpoint of segment 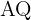

3  is the midpoint of segment
is the midpoint of segment 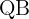
If you have any questions, remember that at Superprof you can find the ideal math teacher for you, whether it's an online math teacher or an instructor for in-person classes.


