The laws of logarithms are a straightforward set of rules that simplify the manipulation of logarithmic expressions. These powerful solutions help us break down complex problems, combine or split logarithms, and solve equations involving exponents. So what are logarithms, what are the log laws, and how can you use them all?

The Laws of Logarithms
A fundamental concept in mathematics that often remains shrouded in mystery for many: the laws of logarithms. For those who venture into the realms of mathematics and calculus, the function of a calculator button labeled "log" may hold some familiarity.
There's something to bear in mind when looking at logarithm laws - in all the examples below, we just use "loga", the notation commonly used with logarithms is either "log", when the logarithm function is using base10, or "loga", where "a" is a number, when the logarithm is using a different base.
Any law of logarithms can be applied to any base system, provided there's no change of base in the expression. For example, all these laws apply to base3 numbers as well, as long as you use base3 for every number in your expression.
main log laws you should learn.
Log Law 1: The Product (Addition) Law
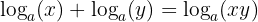
This law uses addition and multiplication properties.
The first law states that adding the logarithms of two numbers (of the same base!) together is the same as taking the logarithm after we multiply the numbers together.
Log Law 2: The Quotient Law
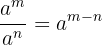
This law uses division and subtraction properties.
The second law states that subtracting the logarithms of two numbers (again, of the same base), is equivalent to dividing the two numbers and taking the logarithm of the result.
Log Law 3: The Power Law
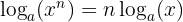
This logarithm law uses exponent properties.
The final logarithm law we'll look at may seem familiar to you - it's very similar to differentiating a term of an expression! The logarithm of a number raised to a power is the same as the whole logarithm being multiplied by that exponent, removing the exponent from the original expression.
Log Law 4: Change of Base Law
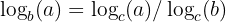
This law allows you to convert a logarithm from one base to another.
The change of base log law is particularly useful because calculators typically only have buttons for logarithms in base 10 (common logarithms, denoted as log) and base e (natural logarithms, denoted as ln), but you might encounter logarithms in other bases in various mathematical problems.
Still confused? Check out this great video explaining logarithms.
The Exponential Function
This is going to be another algebra-heavy topic, so if you're not already comfortable working with algebra, perhaps it's best to brush up on that first or work with a Superprof math tutor, and then come back.
Let's address a special case first. You've probably come across the exponential function already; it's simply written using notation like "ex", and you may see it in an expression like so:
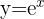
An exponent is the opposite of a logarithm.
In case you aren't too familiar with exponents, they hold a special property that makes them useful. The derivative of "e" (which is short for "exponential form") is equal to itself; that is to say, if we were to differentiate the expression above, we'd end up with the following:
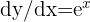
The derivative of the exponent.
When we use logarithms (also known as logarithmic functions), we typically use the "ln" notation to represent what's known as the "natural log" - this is the inverse function of the exponent. What exactly is the exponent? It's what's known as a "constant" because it never changes. "e" represents a specific real number with a lot of decimal places, so it's easier just to represent it using a common notation like a single letter. Just like we do for Pi!

Before we delve into the meaty part of logarithm rules, let's do a quick sample question using natural logs.
Natural Logarithm Example
Here's an example question:
For the exponential equation below, solve for x:
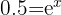
This looks tricky on the face of it, but only because we have an "e" (exponential) thrown into the mix. I think we can all agree that once that's out of the picture, everything will get a lot easier. But how to go about that?
Well, thankfully "ln" has another handy property: it's the inverse of "e", this means that by adding it into our equation, we can cancel out the exponential - just like you might divide an equation by a number to get rid of a coefficient.
Let's do that now:
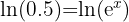
Remember, with equations, everything we do on one side of the equation has to be done on the other. Now, "ln" and "e" are going to cancel each other out, just like multiplying and then dividing by the same number would.
Once that's out of the way, we'll have our answer:
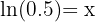
Our exponential equation has now been solved! We don't need to do anything else with the ln(...), as this represents a real number - put it into any graphing or scientific calculator and see!
Looking for math tutors near me? Find one today on Superprof!

Summary Table: The 7 Laws of Logarithms
| Rule Name | Log Rule Equation | Explanation |
|---|---|---|
| Product Rule | 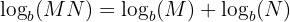 | Log of a product is the sum of the logs. |
| Quotient Rule | 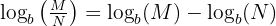 | Log of a quotient is the difference of the logs. |
| Power Rule | 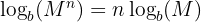 | Log of a power is the exponent times the log. |
| Change of Base Rule | 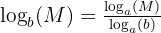 | Allows changing the base of a log to a different base. |
| Zero Exponent Rule | 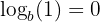 | Log of 1 is always 0, regardless of the base. |
| Log of One | 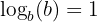 | Log of the base to itself is always 1. |
| Log of Base | 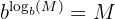 | The base raised to the log of a number returns the number. |

How to Solve Logarithmic Equations
The law logs appear simple in isolation, but unfortunately, it's rarely that easy in an exam. Usually, you'll be faced with the prospect of using any number of combinations of logarithmic functions to come up with an answer.
While this may seem daunting at first, as always, the best way to approach these problems is to tackle them in bite-sized chunks: splitting the question into smaller problems. Solving logarithmic equations involves applying the properties of logarithms and algebraic manipulation. Here's a step-by-step guide:
Remember, solving logarithmic equations may sometimes involve trial and error or multiple steps, so patience and practice are key.

Law Logs Worked Example
Let's examine the log equation below:
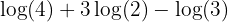
A mixture of logarithm operations making up an expression
Here, all of the terms in our expression are in base10, so we don't specify a base. The question is, how can we simplify this? If you're able to spot the first step, then everything else pretty much works itself out.
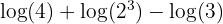
All we've done here is rewrite the second logarithmic function, using the third one of the properties of logarithms that we looked at above. This lets us turn the second term of the expression into a polynomial. The second term we've ended up with (and the second term in the original question both evaluate the same) and are just expressed in different ways. If you don't believe me, you can check on a calculator by entering just the second term of the expression.
Do this once for the term we just created, and once for the original term, and you should see they're both the same value.
Now, at the end of the day, all numbers are numbers: this means that we can take our two to the power of three, and turn it onto 8. Let's do that:
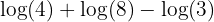
This is starting to look nicer. We're getting closer to just being able to perform simple arithmetic and solve difficult math problems. If you're not sure what's next, take a glance up at the logarithm laws we outlined earlier, and see if you can work out where to go from here.
The next step is to simplify even further, by removing another term. We can now use the first logarithm law we learnt, that adding two logarithms together is the same as multiplying their numerical terms. Once we've done this, we'll be left with two logarithms. We're nearly there!
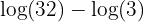
We've multiplied the first two numbers together to make 32, and simplify our expression into two logarithms.
Take a look above, you'll see there's only one law left that we haven't used, and hopefully you'll also see that it fits the final stage of our problem perfectly! We can now subtract the two logarithms:
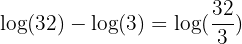
We can't simplify that fraction anymore, so our final answer becomes:
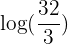
And we're done!
Real-World Applications of Logarithms
When learning about log laws, it can be easier to find motivation by seeing how they're instrumental. In science, engineering, and everyday life, we use logs.
The pH scale in chemistry measures acidity using a base-10 logarithmic scale. Each whole-number change is a tenfold change in hydrogen ion concentration. In physics and sound engineering, decibels are a logarithmic scale that represents sound intensity. Considerable variations in volume can be expressed as manageable numbers. Earth scientists can use the Richter scale to quantify the magnitude of earthquakes. Each step is around 32 times greater in terms of energy released.
Logarithms can be used to analyze algorithms, especially for data complexity or storage growth. Even humans tend to work logarithmically without consciously doing so. For example, how we perceive brightness and loudness (hence the decibel system) changes in proportion to relative differences rather than absolute ones.
Learning about logs might initially be for passing some exams, but there are a lot of applications for them, and many different fields require an understanding of them, so you might still be using them in your academic and professional future.
Wrapping Up the Rules of Logs
The good news is that the laws of logarithms or the rules of logarithms (there's no such thing as the math police as far as we're aware) are fairly simple in their own right. All you really need is a sound understanding of basic arithmetic, and you're well on your way. Where it gets trickier is combining these laws to solve more complex problems.
Logarithms are likely to come up frequently when you're faced with calculus questions, so make sure you're comfortable using them.

If you do find yourself struggling, you might want to consider using Superprof to find math tutors who can give you a helping hand in remembering these identities. Don't worry if you're unsure of something; lots of students struggle with all sorts of mathematics problems, from trigonometry to solving quadratic equations!
As always in math, practice makes perfect! Although these mathematical concepts don't seem like much on their own, they all add up to be essential logs in a large machine! If you fancy some extra activities involving logarithmic equations and exponent functions, try graphing e(x) and ln(x), and see if you can spot any patterns.
As well as logarithms, you can find math help in calculus and mechanic forces for any education level!
Résumer avec l'IA :
















I have appreciated your contribution and I would like to be a participant and a partaker.