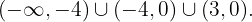Chapters
Let's remember that the domain of a function or output set refers to: all the values that can be assigned to the independent variable without the function becoming indeterminate. Here, we will study the domain of real functions, that is, functions whose domain and range are real numbers or subsets of them.

Domain of Polynomial Functions
Find the domain of the following polynomial functions:
1 
2 
3 
4 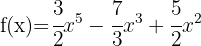
5 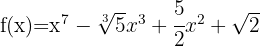
The domain of an entire polynomial function is  , that is, all real numbers.
, that is, all real numbers.
1

2 

3 
Note that this is a polynomial function with rational coefficients: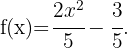
Therefore, 
4 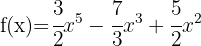
Note that this is a polynomial function with rational coefficients, therefore,
5 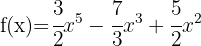
Note that this is a polynomial function with rational and irrational coefficients, therefore, 
Domain of Rational Functions
Calculate the domain of the following rational functions
1 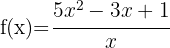
2 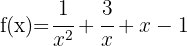
3 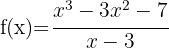
4 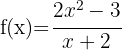
5 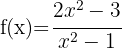
6 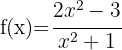
7 
8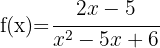
9 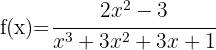
10 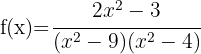
The domain of a rational function is  minus the values that make the denominator zero. To find the domain, we must set the denominator equal to zero and solve the equation. The solutions to that equation are the points that do not belong to the domain, since they make the denominator zero.
minus the values that make the denominator zero. To find the domain, we must set the denominator equal to zero and solve the equation. The solutions to that equation are the points that do not belong to the domain, since they make the denominator zero.
1 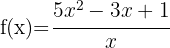
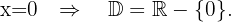
2 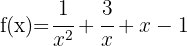
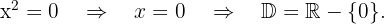
3 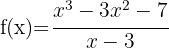

4 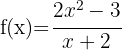

5 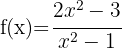

6 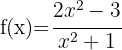
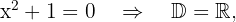
because this equation has no real roots.
7 

because the root is double.
8 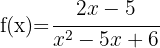
We have that 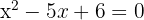 , then
, then
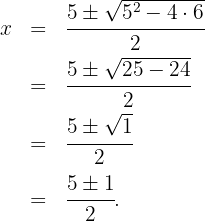
Thus,  or
or 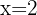 . Therefore, the domain is
. Therefore, the domain is 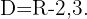
9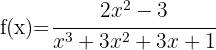
We observe that the polynomial is the expansion of a binomial cubed 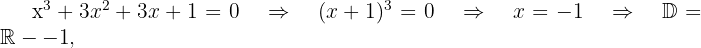
because  is a triple root.
is a triple root.
10 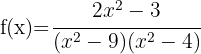
Factoring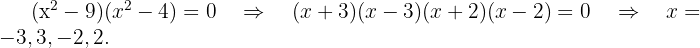
Therefore, 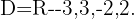
Domain of Functions with Radicals
Find the domain of the following radical functions:
1 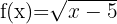
2 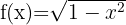
3 
4 
5 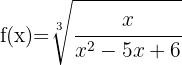
6 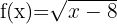
7 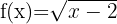
8 
9 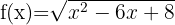
10 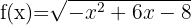
11 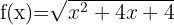
12 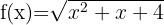
13 
14 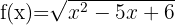
15 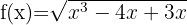
16
17 
18 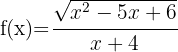
19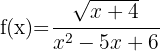
20 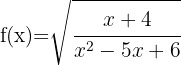
The domain of an irrational function with odd index is 
The domain of an irrational function with even index is obtained from the points that satisfy that the radicand is greater than or equal to zero.
1 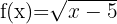
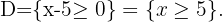
2 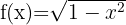
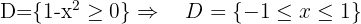
3 

4 
The domain of this function is all reals minus the values where the denominator of the rational function inside the cube root becomes zero. Thus,
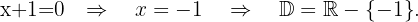
5
The domain of this function is all reals minus the values where the denominator of the rational function inside the cube root becomes zero. Thus,

6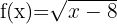
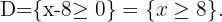
7 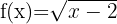
We solve the inequality
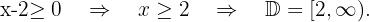
8 
We solve 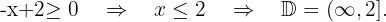
9 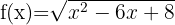
We solve 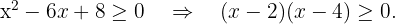
We set equal to zero to obtain the roots 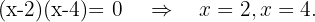

Finally, we take the intervals where the inequality is positive. The union of these will be our domain. Therefore 
10 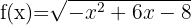
We solve 
We set equal to zero to obtain the roots 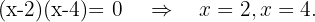
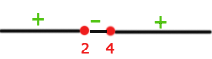
Finally, we take the intervals where the inequality is non-positive. The union of these will be our domain. Therefore 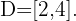
11 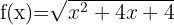
We solve  because
because 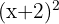 is always greater than or equal to zero.
is always greater than or equal to zero.
12 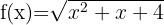
We solve 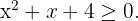
If we set equal to zero, the corresponding equation has no real solutions. Furthermore, we note that for any value taken it will be positive or zero. Therefore, 
13 
We solve 
Note that this inequality is only satisfied for the value  since for all other values of
since for all other values of  , the result is always negative. Thus,
, the result is always negative. Thus,  is the only value that satisfies our inequality and therefore,
is the only value that satisfies our inequality and therefore, 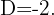
14 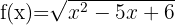
We solve the quadratic inequality

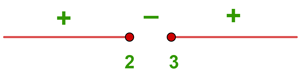
Finally, we take the intervals where the inequality is positive with the endpoints where it equals zero included. The union of these intervals will be our domain. Therefore, 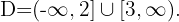
15 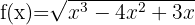
We solve
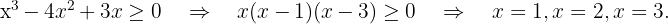

Finally, we take the intervals where the inequality is positive with the endpoints where it equals zero included. The union of these intervals will be our domain. Therefore, 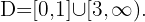
16 
Since the root is in the denominator, the radicand must be greater than zero, but not equal because then it would make the denominator zero.
We solve 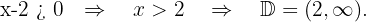
17 
In this case, the denominator must be non-zero and the root in the numerator must be greater than or equal to zero.
We solve 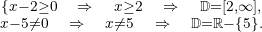
The solution is the intersection of the two sets, therefore, 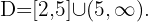
18 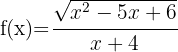
The numerator must be greater than or equal to zero and the denominator must be non-zero.
We solve 
![]()
The solution is the intersection of the two sets, therefore, 
19 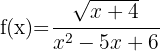
The numerator must be greater than or equal to zero and the denominator must be non-zero.
We solve 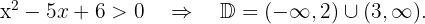
20 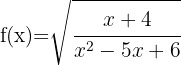
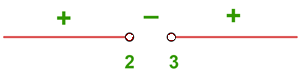
The radicand must be greater than or equal to zero and the denominator must be non-zero.
We solve 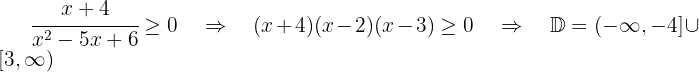 y
y 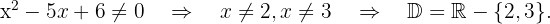
![]()
Using sign analysis with critical points at 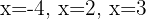 , we get
, we get 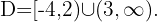
Domain of Exponential Functions
Calculate the domain of exponential functions:
1 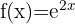
2 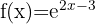
3 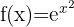
4 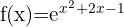
5 
The domain of an exponential function is 
1 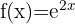

2 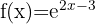

3 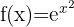

4 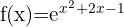

5 
Since the exponent is rational,  does not belong to the domain because it makes the denominator zero. Therefore,
does not belong to the domain because it makes the denominator zero. Therefore, 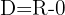 .
.
Domain of Logarithmic Functions
Calculate the domain of logarithmic functions
1 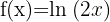
2 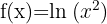
3 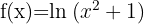
4 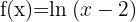
5 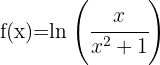
For the logarithm function to be well defined, its argument must be positive, that is, its domain is 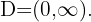
1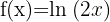
We solve 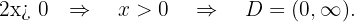
2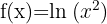
Since  is always positive for
is always positive for 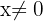 , then
, then 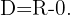
3 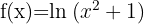
Since 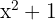 is always positive, then
is always positive, then 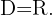
4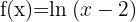
We solve 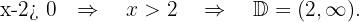
5 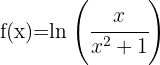
Since the denominator is always positive, we only study the numerator. Thus
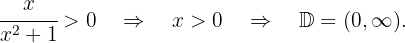 .
.
Domain of Trigonometric Functions
Calculate the domain of trigonometric functions:
1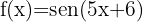
2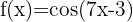
3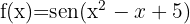
4 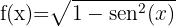
5 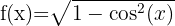
1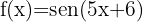
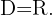
2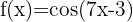
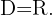
3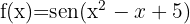
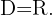
The domain of an irrational function with an even index is formed by the set of values that make the radicand greater than or equal to zero. The trigonometric functions sine and cosine have all real numbers as their domain. Additionally, their maximum value is 1, so these functions always have values less than or equal to 1 for every real number.
4 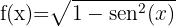
We solve 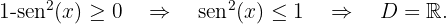
5 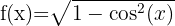
We solve 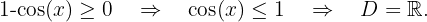
Domain of Piecewise Functions
Calculate the domain of the piecewise function:
1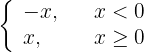
2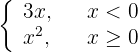
3
4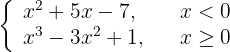
5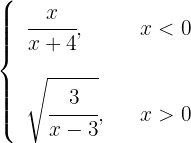
1 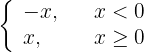
Since each piece is polynomial, then
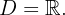
2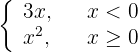
Since each piece is polynomial, then
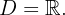
3
Since each piece is polynomial, then
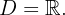
4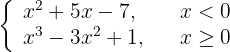
Since each piece is polynomial, then
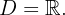
5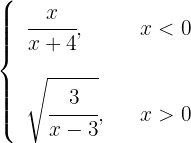
In the first piece, the denominator must be non-zero. In the second piece, since 3 is a constant it will always be positive, we only need to study that the denominator is greater than zero. Thus,
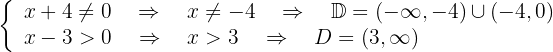
Finally, the solution is