Welcome to our page dedicated to solved exercises on function graphs! If you're interested in understanding how mathematical functions can be visualized and analyzed graphically, you've come to the right place.
In this space, we will explore key concepts related to the graphical representation of linear and quadratic functions. We will provide you with a variety of practical exercises and step-by-step explanations to help you develop your skills in this fascinating field.
In these exercises you will need to graph or analyze function graphs to extract fundamental information about their behavior, a combination that will undoubtedly make you an expert in this area. Let's dive into these interesting exercises!
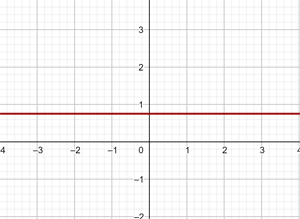
Graph the following lines:
1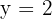
2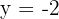
3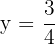
4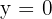
5
6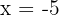
7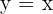
8
9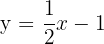
10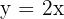
1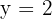
2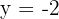
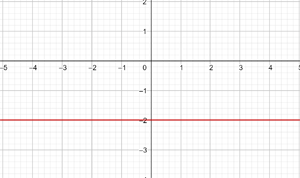
3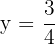
4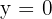
5
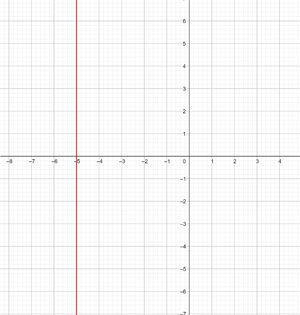
6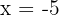
7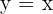
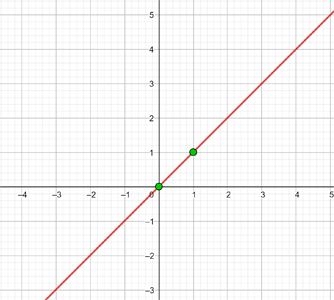
| x | y = x |
|---|---|
| 0 | 0 |
| 1 | 1 |
8
| x | y = -2x - 1 |
|---|---|
| 0 | -1 |
| 1 | -3 |
9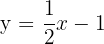
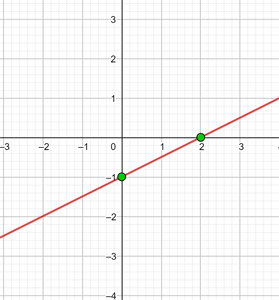
| x | |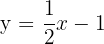
|---|---|
| 0 | -1 |
| 2 | 0 |
10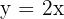
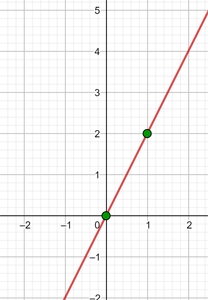
| x |  |
|---|---|
| 0 | 0 |
| 1 | 2 |
Graph the following functions, knowing that:
1) It has slope 
and y-intercept 
.
2) It has slope 
and passes through the point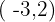 
.
3) It passes through the points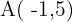 
and 
.
4) It passes through the point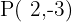 
and is parallel to the line with equation 
.
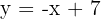1 It has slope and y-intercept .
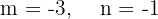
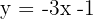
| x |  |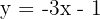
|---|---|
| 0 | -1 |
| 1 | -4 |
2 It has slope and passes through the point (−3, 2).
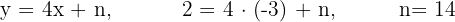
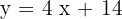
| x |  |
|---|---|
| 0 | 14 |
| 1 | 18 |
3 It passes through the points 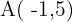and .
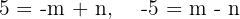
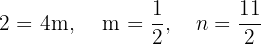
| x |  |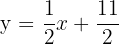
|---|---|
| 0 |  |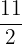
| 1 | 6 |
4 It passes through the point 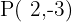and is parallel to the line with equation .
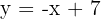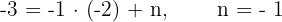
| x |  |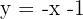
|---|---|
| 0 | -1 |
| 1 | -2 |
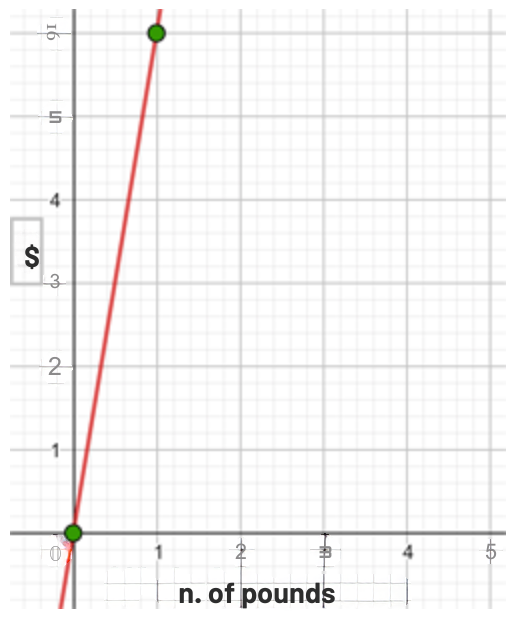
Three pounds of anchovies cost $
. Write and graph the function that defines the cost of anchovies as a function of pounds purchased.
The y-intercept is 
which corresponds to the value of pounds.
The slope is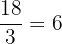 
The equation of the line is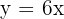 
In the first 
weeks of growing a plant, which measured 
cm (0.79 inches), it has been observed that its growth is directly proportional to time, seeing that in the first week it has grown to measure 
cm (0.98 inches). Establish a function that gives the height of the plant as a function of time and graph it
Initial height 
cm (0.79") is the y-intercept
Weekly growth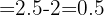 
is the slope
The equation of the line is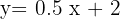 
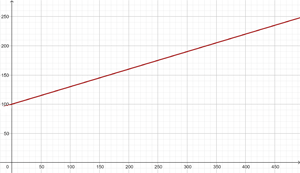
For renting a car they charge $
daily plus $
per mile. Find the equation of the line that relates the daily cost with the number of miles and graph it. If in one day a total of 
miles has been traveled, what amount must we pay?
The y-intercept is and the slope is
The equation of the line is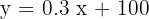 
The amount to pay for traveling miles in one day is:
$
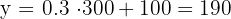An event hall offers its services in a single plan for people at a cost of $
. Additionally, the hall's policy states that if people are exceeded, they will charge $
per extra person. Write and graph the function that defines these costs. Use this function to calculate an overage of 
people
Since we know that the plan has a cost of $ regardless of whether there are or fewer people, then we are dealing with the constant function
Now, for each extra person, the hall charges $. That is, after people, our function ceases to be constant and becomes a linear function whose slope is , which corresponds to the extra cost per person. Thus, our function, which has extra people as the independent variable, is
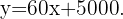
As we can easily verify, $
, which corresponds to people and
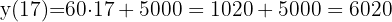$ which corresponds to the total cost for an overage of people.
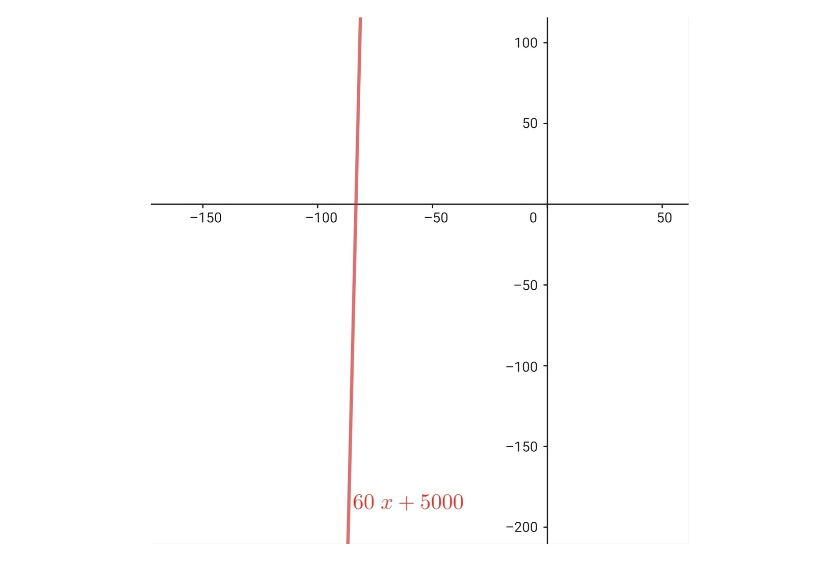
A beach house, with availability for 
people, has a cost per night of $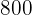
. Additionally, a reservation of a minimum of 
nights is required with an open option to rent the property more nights at a cost of $
each. Write and graph the function that models this situation. A group of friends decides to rent the property and wishes to extend their stay more nights. How much should they pay in total?
The minimum number of nights required when renting the property is . If each night has a cost of $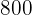, the total for the reservation of is $
. This can be modeled with the constant function
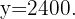
Each extra night has a cost of $. To incorporate this factor, we must move to a linear function.
The linear function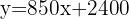 
models our problem. Here the independent variable 
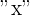corresponds to the number of extra nights.
If the group of friends decides to extend their stay in the house nights, then this corresponds to
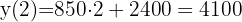$ as the total cost for the 
nights.
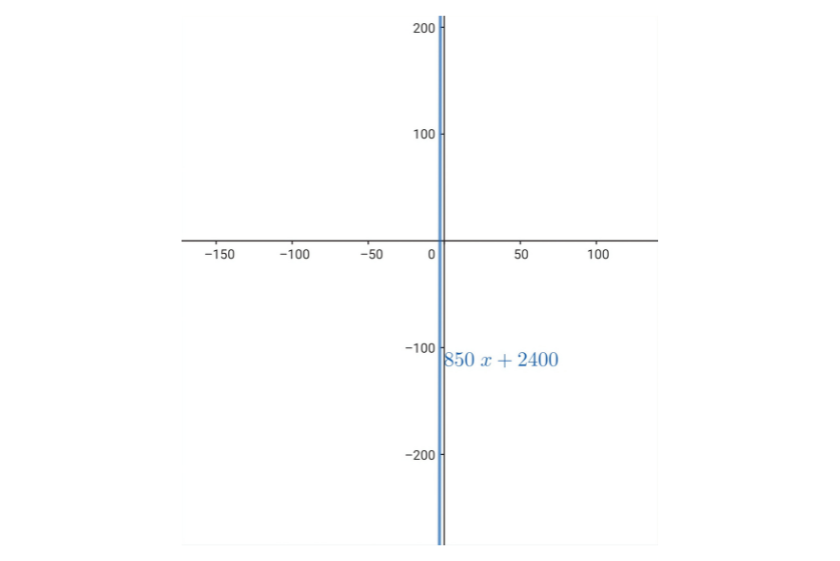
Find the vertex and the equation of the axis of symmetry of the following parabolas:
1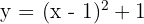
2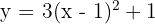
3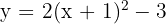
4
5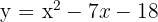
6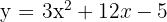
1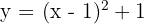
Vertex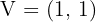 
Axis of symmetry 
2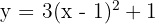
Vertex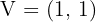
Axis of symmetry
3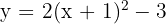
Vertex 
Axis of symmetry 
4
Vertex 
Axis of symmetry 
5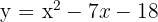
Vertex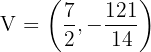 
Axis of symmetry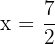 
6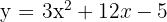
Vertex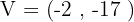 
Axis of symmetry 
Indicate, without graphing them, at how many points the following parabolas intersect the x-axis:
1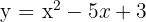
2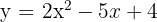
3
4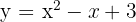
1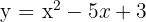
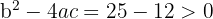
Two intersection points
2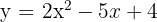
No intersection points
3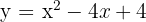 
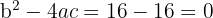
One intersection point
4
Two intersection points
Graph the quadratic functions:
1
2
1
We calculate the coordinates of the vertex
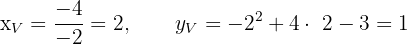
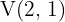
We find the intersection points with the 
axis
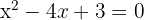
We find the intersection point with the 
axis
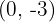
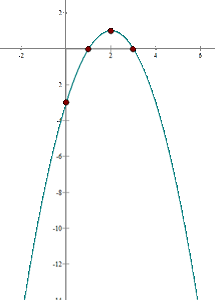
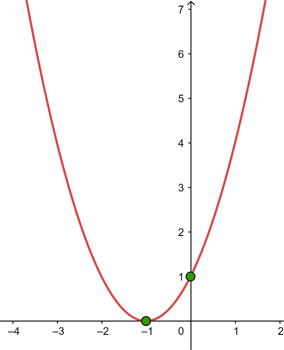
2
We calculate the coordinates of the vertex
We find the intersection points with the axis
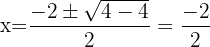
Coincides with the vertex: 
We find the intersection point with the axis
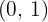
A quadratic function has an expression of the form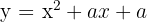 
and passes through the point 
. Calculate the value of 
We substitute the point into the function
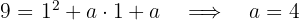
It is known that the quadratic function with equation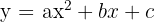 
passes through the points 
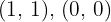and 
. Calculate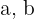 
and 
We substitute the value of each point into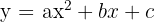
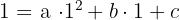
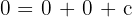
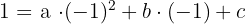
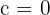
We solve the system by elimination
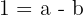
The quadratic function is: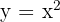 
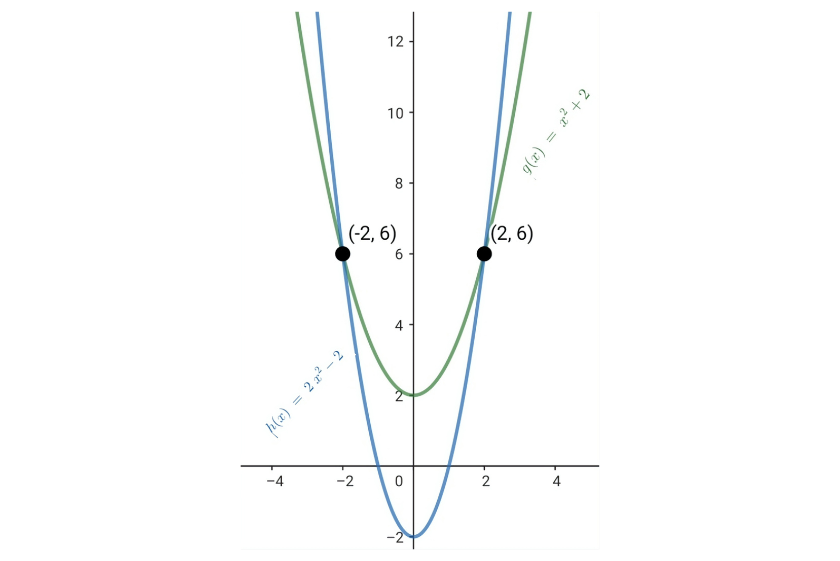
Consider the quadratic functions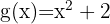 
and 
. Calculate their intersection points
To find the intersection points of these quadratic functions we must equate both functions. Thus we have that
Now, we substitute these values of 
into either of the quadratic functions:
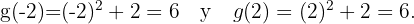
Therefore, the intersection points of the quadratic functions are:
Did you like this article? Rate it!
Loading...
