Chapters

What Is Infinity and How Do We Solve Limit Exercises?
When solving limits we frequently need to operate with infinity. However, we must remember that infinity is not a number. On some occasions we will operate with it as a number in order to find limits, nevertheless, we must keep in mind that on many occasions infinity does not behave like a number.
There are some occasions where operations with infinity are indeterminate. This is one of those occasions where  does not behave like a number. When we encounter some of these indeterminate operations, we must make a slight modification to the function for which we are calculating the limit in order to avoid the indetermination. This is known as "avoiding the indetermination."
does not behave like a number. When we encounter some of these indeterminate operations, we must make a slight modification to the function for which we are calculating the limit in order to avoid the indetermination. This is known as "avoiding the indetermination."
The epsilon-delta definition of a limit is the following:
A value  is the limit of function
is the limit of function 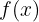 at
at  if for every
if for every 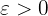 there exists a
there exists a 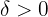 such that for every
such that for every  that satisfies
that satisfies 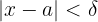 it holds that
it holds that 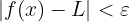 .
.
Verifying that the criteria of the definition are met is one way to prove that the limit exists for a function at a given  .
.
Limits of a Function Raised to Another Function
Let's remember that the definition of  is:
is:
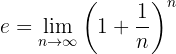
In some cases where we have an indeterminate form of the type  it will be necessary to rewrite the expression in a form similar to the definition of
it will be necessary to rewrite the expression in a form similar to the definition of  ; this way we can calculate the limit.
; this way we can calculate the limit.
Limits with Forms That Are Not Indeterminate
The forms  ,
,  ,
, 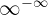 and
and 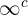 for some
for some 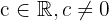 are not indeterminate forms. If we obtain any of these forms we can calculate the limit with confidence.
are not indeterminate forms. If we obtain any of these forms we can calculate the limit with confidence.
Limit Exercises
Using the definition of limit (epsilon-delta), prove that
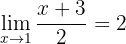
Let's consider an arbitrary 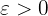 . We must prove that there exists a
. We must prove that there exists a 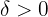 that satisfies the definition of limit.
that satisfies the definition of limit.
We wish that when <
< 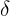
(which we don't know yet), it holds that:
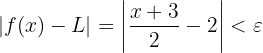
If we simplify a bit, we have:

Note that we are trying to isolate
on one side of the inequality so we can obtain an expression for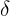
If we multiply both sides of the inequality by 2, we will get:
 <
< 
Therefore, if we take 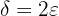
the inequality is satisfied. With this we finish the proof.
What does this mean?
It means that for any 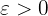 that we are given, we can always find a
that we are given, we can always find a 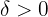 that satisfies the definition because we already have the formula for it—
that satisfies the definition because we already have the formula for it—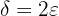 in this case.
in this case.
For example, if we had 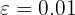 ,
,
then  .
.
Therefore, if  <
< 
is equivalent to
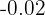 <
<  <
< 
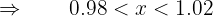 .
.
That is, .
.
Therefore, if we take any  in the interval
in the interval 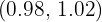 it will hold that
it will hold that
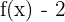 <
< 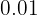
For example, let's take 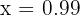 ,
,
then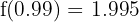 .
.
This way:
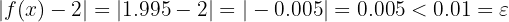
Similarly, if we take 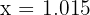 ,
,
Then 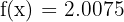 .
.
Therefore:
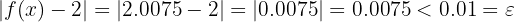
Observe the following graph of  and determine the requested limits:
and determine the requested limits:
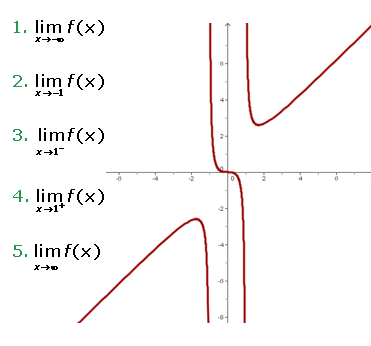
1 The first limit we are asked for is
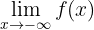
Notice that when 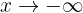 , that is, when
, that is, when  decreases "infinitely," the function also decreases infinitely. Therefore,
decreases "infinitely," the function also decreases infinitely. Therefore,
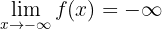
2 Now we are asked to determine
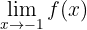
In this case let's observe that when  approaches
approaches  very closely from the left, the function decreases infinitely. On the other hand, when
very closely from the left, the function decreases infinitely. On the other hand, when  approaches
approaches  very closely from the right, the function increases infinitely. Therefore, we can conclude that the limit does not exist.
very closely from the right, the function increases infinitely. Therefore, we can conclude that the limit does not exist.
3 Now we are asked to calculate
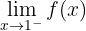
which refers to the left-hand limit. Let's observe that when  approaches
approaches  from the left, the function decreases infinitely. Therefore, the limit is
from the left, the function decreases infinitely. Therefore, the limit is
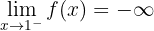
4 The fourth limit is

which is now the right-hand limit. Therefore,
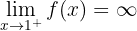
5 Finally we are asked for the limit

which is very similar to the first limit. We can observe that as  grows indefinitely,
grows indefinitely,  also grows indefinitely. Therefore,
also grows indefinitely. Therefore,
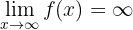
Calculate the limit

We want to find the limit
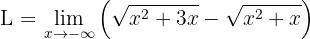
Notice, first, that if we "evaluate at infinity," we obtain an indeterminate form:
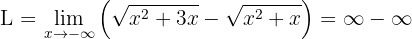
Since the value of  is not determined, we need to perform an algebraic manipulation of our function.
is not determined, we need to perform an algebraic manipulation of our function.
Before doing the algebraic manipulation, let's transform the limit using the property:
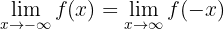
With which the limit becomes:
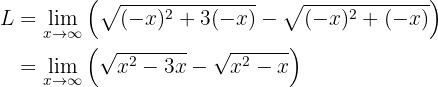
Now we need to algebraically manipulate the limits in order to eliminate the subtraction of infinities. This is achieved by "rationalizing" (that is, multiplying and dividing by the conjugate):
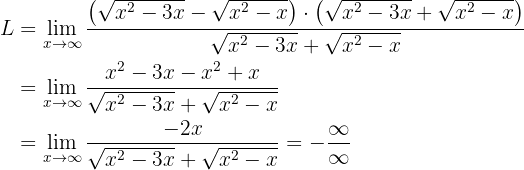
Notice that if we evaluate at infinity, we again have a new indetermination. In this case it's an indetermination 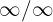 . To get rid of this indetermination we must perform another algebraic manipulation. In this case it's multiplying and dividing by
. To get rid of this indetermination we must perform another algebraic manipulation. In this case it's multiplying and dividing by 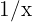 :
:
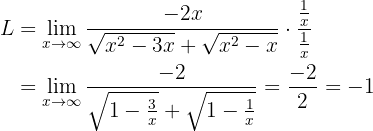
Which is the result we were looking for.
Calculate the limit
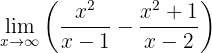
Now we have the limit:

Notice that if we evaluate at infinity directly, we obtain:
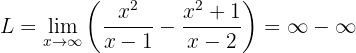
To get rid of this indetermination we can add the fractions (using the common denominator):
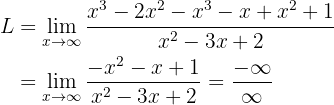
Since we now have an indetermination of the form 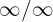 , we will look to multiply and divide by an appropriate term to avoid the indetermination. The appropriate term is the monomial of highest degree in the numerator or denominator, that is,
, we will look to multiply and divide by an appropriate term to avoid the indetermination. The appropriate term is the monomial of highest degree in the numerator or denominator, that is, 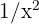 . Therefore, we have:
. Therefore, we have:
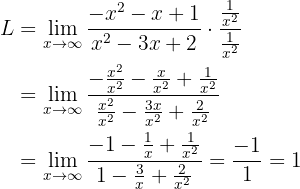
So the limit is  .
.
Calculate the limit

If we evaluate at infinity, we obtain the following:
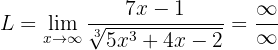
This is an indetermination of 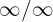 . Therefore, we must multiply and divide by the monomial of highest degree (either in numerator or denominator). In this case it's
. Therefore, we must multiply and divide by the monomial of highest degree (either in numerator or denominator). In this case it's 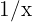 —since the denominator involves a cube root, then the "monomial"
—since the denominator involves a cube root, then the "monomial"  is considered as a monomial of degree 1—. Thus:
is considered as a monomial of degree 1—. Thus:
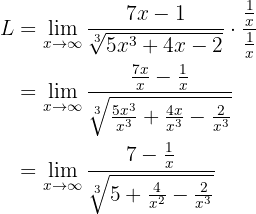
When we "evaluate at infinity" we have:

Evaluate the limit
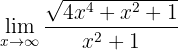
If we evaluate the function at infinity, we obtain:

Therefore, being an indeterminate form, we must multiply and divide by the monomial of highest degree ( ; remember that we divide the powers of the numerator by 2 since they are inside a square root):
; remember that we divide the powers of the numerator by 2 since they are inside a square root):
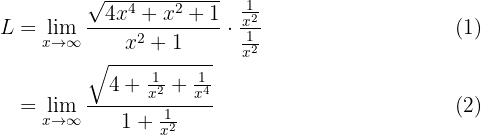
Then, evaluating at infinity, we have:
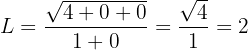
Therefore, the limit is 2.
Evaluate the limit
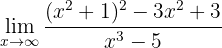
If we evaluate the function at infinity, we can immediately see that:
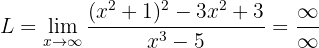
Therefore, we must perform an algebraic manipulation to get rid of the indetermination.
This limit can be solved in two ways.
1 By comparison of infinities:
First we expand the binomial squared, thus we obtain

Notice that in the numerator we obtain  while in the denominator we have
while in the denominator we have  as the highest degree terms. Consequently, the degree of the numerator is greater and the limit will be
as the highest degree terms. Consequently, the degree of the numerator is greater and the limit will be  . Remember that when the degree of the numerator is greater, then the limit is
. Remember that when the degree of the numerator is greater, then the limit is  if the highest degree terms have the same sign.
if the highest degree terms have the same sign.
2 Dividing numerator and denominator by the highest degree term:
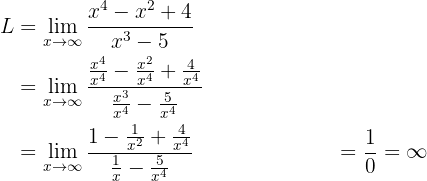
Notice that, in general,  is an indeterminate form. However, we are calculating a limit when
is an indeterminate form. However, we are calculating a limit when  , furthermore, both the numerator and denominator are positive as
, furthermore, both the numerator and denominator are positive as  grows. Therefore, we can conclude that the limit will be
grows. Therefore, we can conclude that the limit will be  .
.
Calculate the limit

If we evaluate at infinity, we have:

However, the infinity in the denominator has a higher order. Therefore, we can conclude that 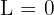 .
.
Nevertheless, proving that the limit is 0 without using L'Hôpital or the "order" criterion is complicated. To do it, let's denote:
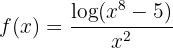
To find the limit, we must look for two functions  and
and  such that
such that  and
and

If we find these functions, then we can conclude that 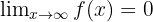 .
.
First, let's observe that when 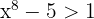 , then
, then 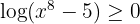 (and this holds when
(and this holds when  is large). Similarly, we have that
is large). Similarly, we have that  for
for 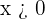 . Therefore, we have that:
. Therefore, we have that:
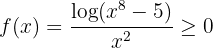
when  "is sufficiently large." Thus, we have that
"is sufficiently large." Thus, we have that 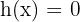 where it's clear that
where it's clear that 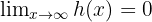 .
.
To find the second function, first notice that 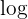 is an increasing function, therefore, since
is an increasing function, therefore, since  , then
, then  . Thus, we have that
. Thus, we have that
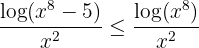
now, if we take 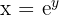 , then we can write
, then we can write
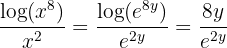
A very important property about the exponential function is
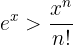
for any  and
and 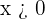 . If we take
. If we take 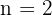 , then we have
, then we have

From this it follows that
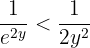
Therefore, we have that
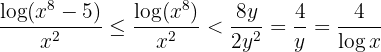
Thus, 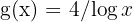
where  .
.
Furthermore, 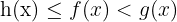 .
.
Therefore, 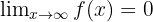 .
.
Calculate the limit
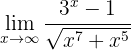
If we evaluate at  , then we obtain
, then we obtain
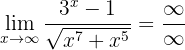
Here we can also observe the "order" of the denominator and numerator to determine the limit. In this case the numerator has a limit of higher order, therefore,
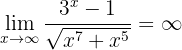
To prove it, let's denote

and we must find a function  such that
such that 
and 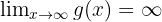 .
.
First, let's observe that when  ,
,
then 
(that is, the radicand is positive for a sufficiently large  ).
).
Furthermore, 
when  ,
,
therefore
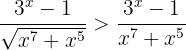
Now notice that if  , then
, then 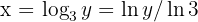 . From this it follows that
. From this it follows that

Therefore, 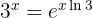 . Similarly, since we know that
. Similarly, since we know that
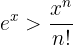
when x > 0, then we have that
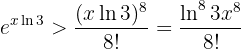
Thus, we have that
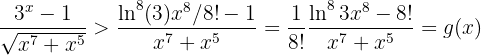
where 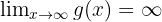 . Therefore, the limit is
. Therefore, the limit is
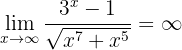
Calculate the limit
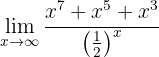
When evaluating at infinity, we have that

Therefore, the limit must be infinity, since both the numerator and denominator are positive for a sufficiently large  . To see it more clearly, notice that
. To see it more clearly, notice that
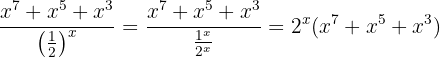
Thus,
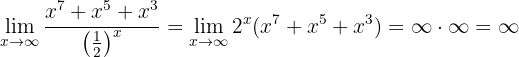
Calculate the limit
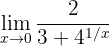
If we evaluate at 0, we have

where we have an indeterminate form of the type  . Notice that in this case we cannot say that
. Notice that in this case we cannot say that  since we are calculating a limit when
since we are calculating a limit when 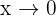 and
and  is positive or negative near 0 (when calculating limits
is positive or negative near 0 (when calculating limits  this is usually not a problem).
this is usually not a problem).
Therefore, we must calculate the one-sided limits:
1 First we calculate the left-hand limit
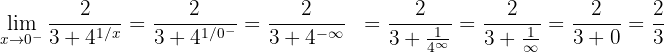
2 Now we calculate the right-hand limit
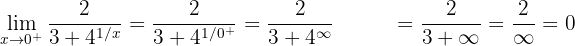
Here we can observe that the two one-sided limits are different, therefore, the limit when 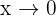 does not exist.
does not exist.
Calculate the limit
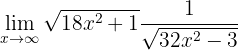
If we "evaluate at infinity," we obtain

Therefore, we must perform an algebraic manipulation. First let's write the limit as a single fraction:
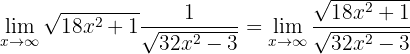
Now let's divide the numerator and denominator by the highest degree coefficient (that is  since it's inside a square root):
since it's inside a square root):
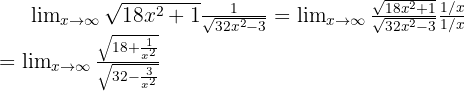
Now we can evaluate at infinity, so we obtain:
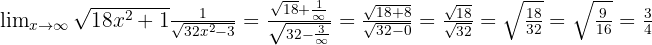
Therefore, the limit is 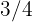 .
.
Find the limit
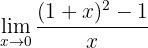
If we evaluate at 0, we can observe that
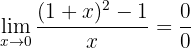
so we have an indetermination and need to perform an algebraic manipulation. For this, we expand the binomial squared:
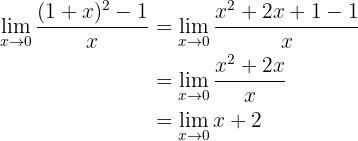
If we evaluate now at 0, we obtain:
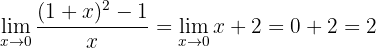
Therefore, the limit is 2.
Evaluate the limit

If we evaluate at 3, we will obtain
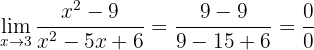
So we can observe that we have, again, an indeterminate form. To avoid the indetermination we will factor both the numerator and denominator (observe that the numerator is a difference of squares; while the denominator can be factored by finding a pair of numbers that when multiplied give 6 and when added give -5):
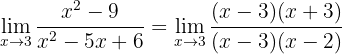
In this way, we can cancel  to have
to have

Thus, the limit is 6.
Calculate the limit
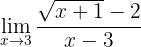
If we evaluate the function at 3, we observe that
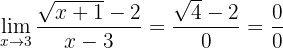
So we have an indetermination and must perform an algebraic manipulation. In this case, since we have an expression with radicals, we must multiply and divide the fraction by the conjugate of the numerator (since it's the one that has the radical):
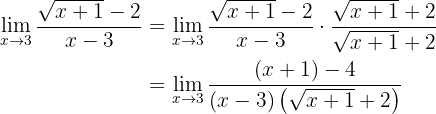
which is obtained because we have "conjugate binomials" in the numerator. Simplifying:
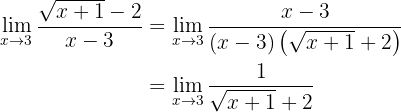
Now we can evaluate at 3, from which we obtain:
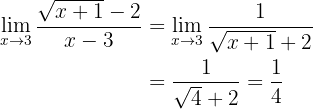
Therefore, the limit is 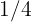 .
.
Calculate the limit

If we evaluate at  , we will obtain:
, we will obtain:

This is an indeterminate form. Therefore, we must perform algebraic manipulations to obtain some expression similar to the definition of  . To do this, we first add and subtract 2 in the exponent (we will denote the limit as
. To do this, we first add and subtract 2 in the exponent (we will denote the limit as  ):
):
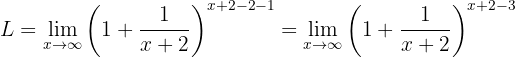
Then we use properties of exponents:

Notice that the first power coincides with the definition of  with
with  . Therefore, the limit is:
. Therefore, the limit is:
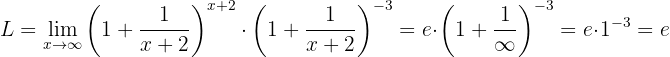
Calculate the limit
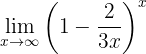
When evaluating at infinity, we have:

Therefore, we must perform an algebraic manipulation to obtain an expression similar to the definition of  . To do this, we first modify the expression we have inside the parentheses (and denote the limit as
. To do this, we first modify the expression we have inside the parentheses (and denote the limit as  ):
):

Therefore, in the exponent we must have 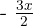 somehow. Notice that this is achieved by doing:
somehow. Notice that this is achieved by doing:

Then we use properties of exponents:
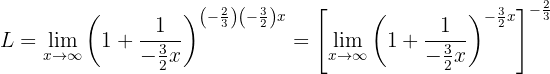
Now we can calculate the limit (noting that what's inside the square brackets is the definition of  with
with 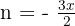 ):
):
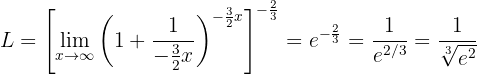
Calculate the limit
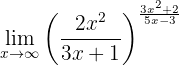
If we evaluate at  , we immediately see that we have:
, we immediately see that we have:
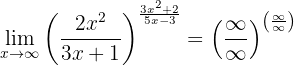
To solve it, we will use comparison of infinities in the two fractions. First notice that
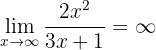
since the numerator is a polynomial of higher degree (and the leading coefficients have the same sign). Similarly,
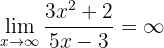
for the same reason. Therefore, the limit is:

since the last expression is not an indeterminate form.
Determine the limit
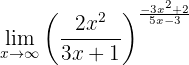
Again, if we evaluate at infinity we will obtain:
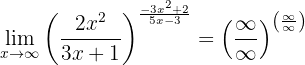
However, if we solve the limits of the fractions (comparing the orders of the infinities), we can observe that:

since the numerator is a polynomial of higher degree and the leading coefficients have the same sign. On the other hand,
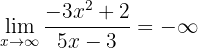
because the numerator is a polynomial of higher degree, but the leading coefficients have different signs. In this way, we have that the limit is:

Determine the following limit:
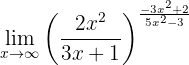
Again, if we evaluate at infinity we have that

Therefore, we evaluate the limits of the fractions separately. In the base of the power we have that the numerator is a polynomial of higher degree, in addition to the leading coefficients having the same sign, therefore

On the other hand, in the exponent both the numerator and denominator are polynomials with the same order. Consequently, the limit is the quotient of the leading coefficients:
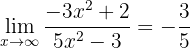
Therefore, the limit is

since  if
if  .
.
Evaluate the following limit:
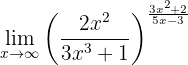
If we evaluate at infinity we have that
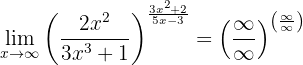
So we have to evaluate the limits of the fractions separately to determine the general limit. We have that
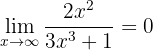
since the denominator is a polynomial of higher degree. Similarly,
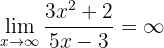
because the numerator is a polynomial of higher degree and the leading coefficients have the same sign. Therefore, the limit is

because 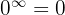 (that is, it's not an indeterminate form).
(that is, it's not an indeterminate form).
Evaluate the following limit:
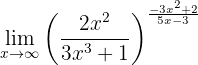
This limit is practically the same as the previous one, with only one sign difference.

So we have to evaluate the limits of the fractions separately to determine the general limit. Just like in the previous case, we have that
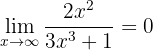
since the denominator is a polynomial of higher degree. Similarly, we have that
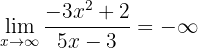
because the numerator is a polynomial of higher degree and the leading coefficients have different signs. Therefore, the limit is

notice that this is an indeterminate form. Therefore, we must use the property:

so
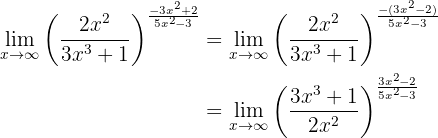
In this case,

So
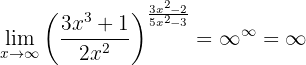
Note: it's important to write it this way. The reason is that  is an indeterminate form (that is, we can construct different functions where that indeterminate form "converges" to a different value).
is an indeterminate form (that is, we can construct different functions where that indeterminate form "converges" to a different value).
Evaluate the following limit:

Just like in the previous cases, if we evaluate at infinity, we obtain

And just like in the previous cases, we calculate the limits of each fraction separately:
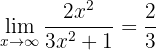
since the numerator and denominator are polynomials of the same degree (so the limit is the quotient of the leading coefficients). Similarly, we have that

so the limit is

Evaluate the following limit:

As in the previous cases, when evaluating at infinity we have
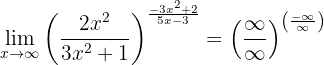
We calculate the limits of each fraction separately:
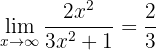
since the numerator and denominator are polynomials of the same degree (so the limit is the quotient of the leading coefficients). Furthermore, we have that
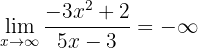
since the numerator is a polynomial of higher degree and the leading coefficients have different signs. Thus, the limit is

since we have an expression of the form 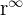 where r > 1.
where r > 1.
Determine the following limit:
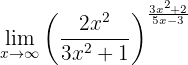
As in the previous cases, when evaluating at infinity we have
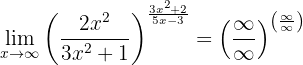
note that the function is practically the same as the previous one, but with only one sign changed. We calculate the limits of each fraction separately:
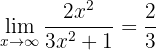
since the numerator and denominator are polynomials of the same degree (so the limit is the quotient of the leading coefficients). Furthermore, we have that
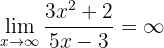
because the numerator is a polynomial of higher degree and the leading coefficients have the same sign. In this way, the limit is
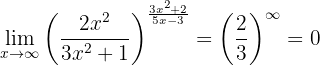
since we have an expression of the form 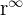 where 0 < r < 1.
where 0 < r < 1.
If you're looking for a math tutor, whether you prefer an online math teacher or one who travels to your home, you'll find the one that best suits you at Superprof.












