Chapters
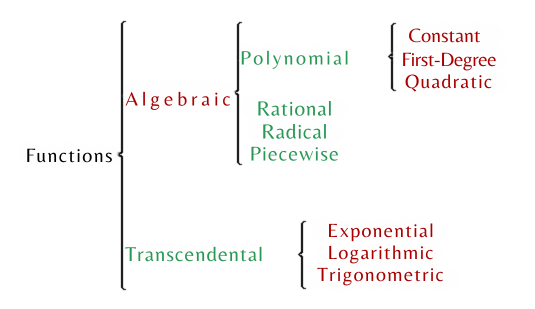
Algebraic Functions
In algebraic functions, the operations that must be performed with the independent variable are: addition, subtraction, multiplication, division, exponentiation, and root extraction.
Algebraic functions can be:
Explicit Functions
If the images of 
can be obtained by simple substitution as in this example: 
Implicit Functions
If the images of cannot be obtained by simple substitution, but operations are necessary, as in this example 
In addition to this classification, there are 6 other types of algebraic functions:
1. Polynomial Functions
- These are functions that are defined by a polynomial.
- Their domain is
, that is, any real number has an image.
2. Constant Functions
- The criterion is given by a real number.
- The graph is a horizontal line parallel to the x-axis.
3. First-Degree Polynomial Functions
Functions of this type include:
Affine function
1 
- Its graph is an oblique line, which is defined by two points of the function.
Linear function
2 
Identity function
3 
Quadratic functions
4 
- These are second-degree polynomial functions.
- The graph of a polynomial function is a parabola.
4. Rational Functions
- The domain consists of all real numbers except the values of x that make the denominator zero.
- The criterion is given by a quotient between polynomials.
5. Radical Functions
- The criterion is given by the variable x under the radical sign.
- The domain of an irrational function with odd index is .
- The domain of an irrational function with even index consists of all values that make the radicand greater than or equal to zero.
6. Piecewise Algebraic Functions
These are functions defined by different criteria, according to the intervals considered.
- Sign function
- Absolute value functions
- Greatest integer function of x
- Mantissa function
Transcendental Functions
The independent variable appears as an exponent, or as the index of a root, or is affected by the logarithm sign or any of the signs used in trigonometry.
1. Exponential Functions
Let a be a positive real number. An exponential function with base 
is a function that assigns to each real number the value 
. In this function, is the base and is the exponent.
2. Logarithmic Functions
The logarithmic function with base a is the inverse function of the exponential function with base a.
3. Trigonometric Functions
Sine Function
Cosine Function
Tangent Function
Cosecant Function
Secant Function
Cotangent Function
Did you like this article? Rate it!
Loading...
