Chapters
Definition of Logarithm
The logarithm of a number, in a given base, is the exponent to which the base must be raised to obtain that number.
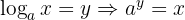
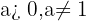
Where 
is the base, 
is the number and 
is the logarithm.
Common and Natural Logarithms
Common logarithms have base 
. They are represented by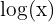 
.
Natural logarithms (also known as Napierian logarithms) have base 
. They are represented by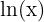 
or 
.
Examples of Using the Definition of Logarithm
Write the Following Logarithms in Exponential Notation
1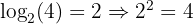 
2 
3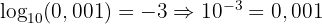 
4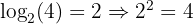
Using the Definition of Logarithm and Algebra, Calculate the Calue of the Unknown in the Following Equations
1 
We apply the definition of logarithm and convert 
to a decimal fraction and simplify it:
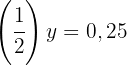
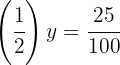
We write 
in the form of a power and equate the exponents
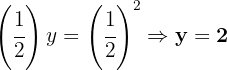
2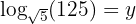 
We apply the definition of logarithm and the root is written in the form of a power with fractional exponent
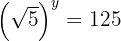
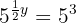
We equate the exponents
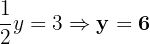
3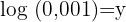 
We apply the definition of logarithm and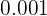 
is converted to a decimal fraction
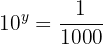
We convert the quotient to a power of base and equate the exponents
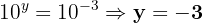
4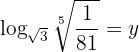 
We apply the definition of logarithm, the roots are written in the form of powers with fractional exponents and the exponents are equated
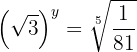
5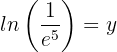 
We apply the definition of logarithm, taking into account that the base of the natural logarithm is .
The fraction is written in the form of a power and the exponents are equated
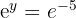
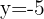
Properties of Logarithms
1 The logarithm of a product equals the sum of the logarithms of the factors
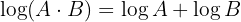
2 The logarithm of a quotient equals the difference of the logarithm of the dividend and the logarithm of the divisor
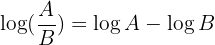
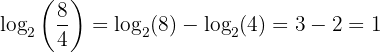
3 The logarithm of a power equals the product of the exponent and the logarithm of the base
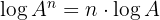
4 The logarithm of a root equals the quotient between the logarithm of the radicand and the index of the root
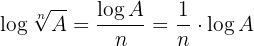
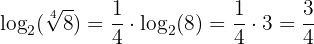
From properties 
and 
we can deduce that:
5 The base '' logarithm of '' is 
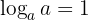
6 The logarithm of is 
(Regardless of the logarithm base)
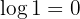
Thus:
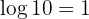
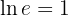
7 The argument of a logarithm must always be greater than zero
For 
it holds that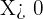 
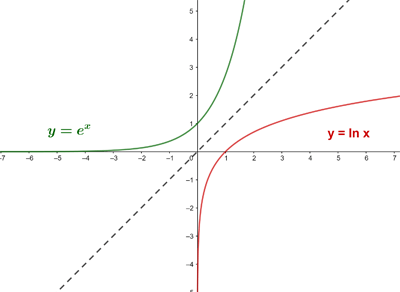
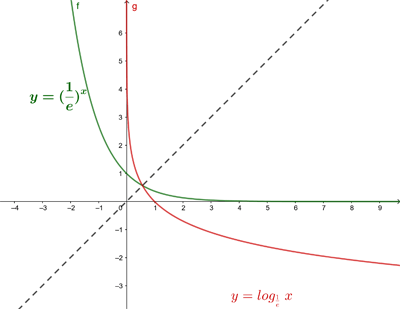
Logarithmic Function
The logarithmic function with base is the inverse function of the exponential with base .
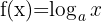
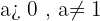
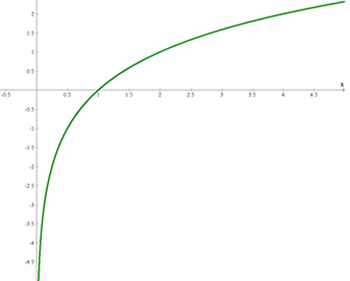
Examples of Logarithmic Functions
|  |
|---|---|
 |  |
 |  |
 |  |
| |
 | |
| |
 | |
|  |
|---|---|
 | |
| |
| |
| |
| |
| |
| |
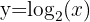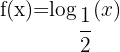
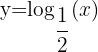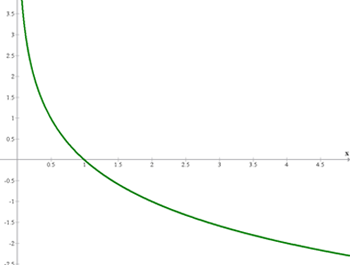
Properties of Logarithmic Functions
- Domain:
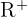
- Range:
- It is continuous
- The points
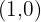and 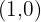belong to the graph. - It is injective (no image has more than one pre-image).
- Increasing if
- Decreasing if
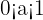
The graph of the logarithmic function is symmetric (with respect to the bisector of the first and third quadrant) to the graph of the exponential function, since they are reciprocal or inverse functions of each other.
Did you like this article? Rate it!
Loading...
