Chapters
- Domain of a Polynomial Function
- Domain of a Rational Function
- Domain of a Radical Function with Odd Index
- Domain of a Radical Function with Even Index
- Domain of a Logarithmic Function
- Domain of an Exponential Function
- Domain of the Sine Function
- Domain of the Cosine Function
- Domain of the Tangent Function
- Domain of the Cotangent Function
- Domain of the Secant Function
- Domain of the Cosecant Function
- Domain of Operations with Functions
The domain of a function consists of all elements that have an image.
These are the values of 
that we can substitute into the correspondence rule of a function to obtain the corresponding value of 
.
Mathematically, we can express:
which means that the domain of a function consists of those values of that belong to the real numbers for which there exists an associated value of the function .
The subset of real numbers on which the function is defined is called the domain or field of existence of the function.
It is denoted by D.
The variable x belonging to the domain of the function is called the independent variable.
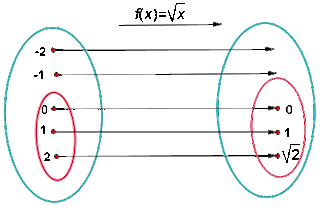
Domain of a Polynomial Function
The domain of a polynomial function is 
, because any real number has an image.
Functions that have a number (a constant) in the denominator are also polynomial functions:
Examples of Domains of Polynomial Functions
1 
2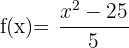 
You can verify that by substituting any value of into these functions you will always obtain a corresponding value for .
Domain of a Rational Function
The domain is minus the values that make the denominator zero (a fraction cannot exist if it has a denominator of zero).
Example Exercise on the Domain of a Rational Function
- What is the domain of the function
?
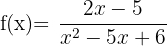We set the denominator equal to 
and solve the equation:
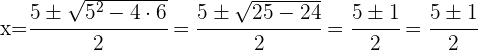
Domain of a Radical Function with Odd Index
The domain is the domain of the radicand function.
1 
2 
Domain of a Radical Function with Even Index
The domain consists of all values of the radicand that make it greater than or equal to zero.
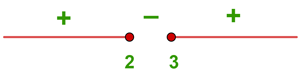
2.
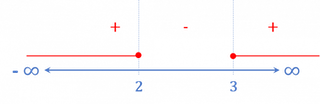
3. What is the domain of the function 
?
In this case, the denominator must be greater than zero and, furthermore, we must find the values of for which the square root exists, so:
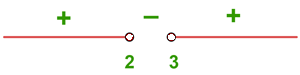
4. Determine the domain of the function .
The radicand must be greater than or equal to zero and the denominator must be different from zero:
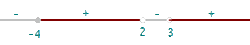
5. Find the domain of the function 
.
Since the radicand must be greater than or equal to zero, we set up the inequality:
We solve the quadratic inequality:
The roots of the quadratic equation associated with the inequality are: 
and 
So the intervals in which the inequality is satisfied would be:
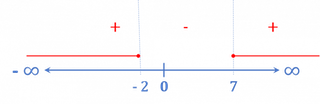
The domain consists of values less than or equal to -2 and greater than or equal to 7, including them.
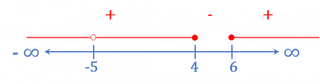
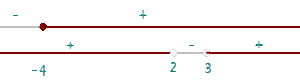
6. Find the domain of the function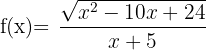 
.
In this case, two conditions must be met, one for the quotient and one for the square root, so the numerator must be greater than or equal to zero and the denominator must be different from zero. Therefore:
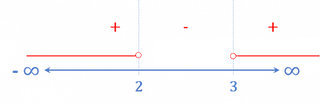
Domain of a Logarithmic Function
The domain consists of all values that make the function inside the logarithm greater than zero.
The following must be satisfied:
Domain of an Exponential Function
Examples of Domains of Exponential Functions
1. 
2. 
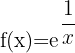
The domain equals minus the values that make the denominator of the exponent zero:
3. 
The domain coincides with the real field of existence of the square root:
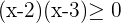
Domain of the Sine Function
The domain of the sine function is
Domain of the Cosine Function
The domain of the cosine function is
Domain of the Tangent Function
Domain of the Cotangent Function
Domain of the Secant Function
Domain of the Cosecant Function
Domain of Operations with Functions
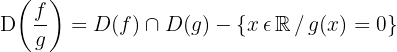
Remember that you can find a private tutor for math courses tailored to your level.
Did you like this article? Rate it!
Loading...
