Chapters
Quadratic Function
Polynomial functions are those consisting of a polynomial. An example of these is the quadratic or second-degree function, represented with a parabola graph and the following equation:
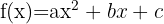
Graphical Representation of the Parabola
To construct a parabola graph, you need to know the following elements:
Vertex
The axis of symmetry of the parabola passes through the vertex. That is, when the coefficient of the term 
is positive, the vertex will be the lowest point of the graph, and the formulas to find it are as follows:
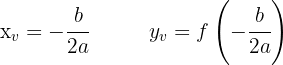
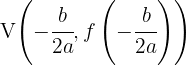
Likewise, the equation of the axis of symmetry is:
Points of Intersection with the X-axis
To find the value of 
when 
, the second coordinate must be set equal to zero, so we must solve the following equality:
When solving the above equation, the results can be:
Two intersection blocks:
and
This happens if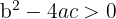 
One intersection point:
This happens if 
No intersection points:
If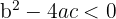 
Point of Intersection with the Y-axis
To find the intersection with the 
-axis, the first coordinate must be set equal to zero, 
, so we will have:
Example
To represent the function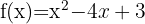 
, it is necessary to find the following elements that make up the parabola:
Vertex
We apply the formulas described in the previous section to find the coordinates of the vertex, which are:
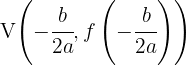
Then the coordinates of the vertex are:
Points of Intersection with the X-axis
To find the point or points of intersection with the X-axis, we set the function equal to 0, as indicated previously:
To solve the equation, we use the quadratic formula for second-degree equations:
In this case, we have found two intersection points, which are: 
and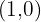 
Point of Intersection with the Y-axis
To find the point of intersection with , it is enough to know the value of the constant 
, which in this case is 
, and the coordinates are: (0,3).
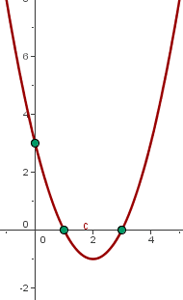
Graph of the Quadratic Function
We start with
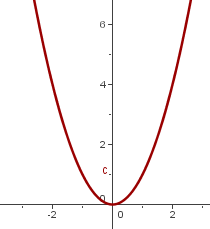
Vertical Translation
If our function is
Where:
- k > 0, then y=x² shifts upward k units.
- k < 0, then y=x² shifts upward k units.
In this case, the vertex of the parabola is: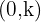 
.
And the axis of symmetry is .
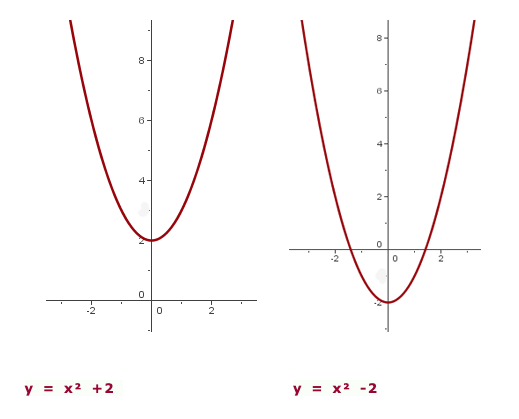
Horizontal Translation
For the equation
Where:
- h > 0, then y=x² shifts upward h units.
- h < 0, then y=x² shifts upward h units.
In this exercise, the vertex of the parabola is: (-h,0).
And the axis of symmetry is x=-h.
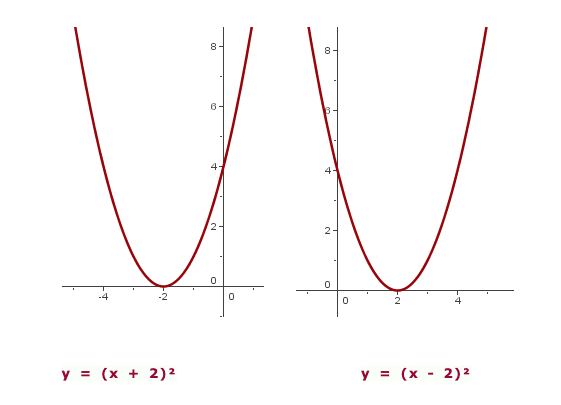
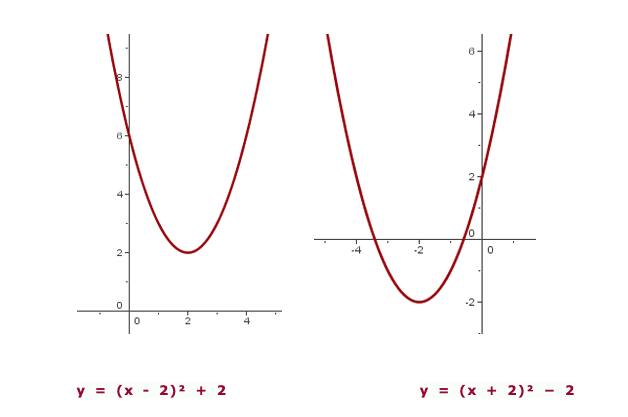
Oblique Translation
Finally, in the following expression:
The vertex of the parabola is: (-h,k).
And the axis of symmetry is x=-h.
Summarize with AI:
Did you like this article? Rate it!
Loading...
